Forecasting diagnostics

BUS 323 Forecasting and Risk Analysis

Fitted values

• Mean method: \(\hat{y}_{t} = \hat{c}\)
  • Where \(\hat{c}\) is the mean of all observations of \(y_{t}\).

Fitted values

• Mean method: \(\hat{y}_{t} = \hat{c}\)
  • Where \(\hat{c}\) is the mean of all observations of \(y_{t}\).
• Drift method: \(\hat{y}_{t} = y_{t-1} + \hat{c}\)
  • Where \(\hat{c}=\frac{y_{T}-y_{1}}{T-2}\).

Residuals

• \(e_{t} = y_{t} - \hat{y}_{t}\)
• Innovation residuals: residuals resulting from a transformation of the data.

Residuals

• \(e_{t} = y_{t} - \hat{y}_{t}\)
• Innovation residuals: residuals resulting from a transformation of the data.
  • e.g. suppose \(w_{t} = log(y_{t})\).

Residuals

• \(e_{t} = y_{t} - \hat{y}_{t}\)
• Innovation residuals: residuals resulting from a transformation of the data.
  • e.g. suppose \(w_{t} = log(y_{t})\).
    • Innovation residuals: \(w_{t} - \hat{w}_{t}\).

Residuals

• \(e_{t} = y_{t} - \hat{y}_{t}\)
• Innovation residuals: residuals resulting from a transformation of the data.
  • e.g. suppose \(w_{t} = log(y_{t})\).
    • Innovation residuals: \(w_{t} - \hat{w}_{t}\).
    • Residuals: \(y_{t} - \hat{y}_{t}\).

Using residuals in R

• After estimating a model(), apply augment() to it.

Using residuals in R

• After estimating a model(), apply augment() to it.
• Here are the models we estimated last time:

library(fpp3)
bricks <- aus_production |>
  filter_index("1970 Q1" ~ "2004 Q4") |>
  select(Bricks)
train <- aus_production |>
  filter_index("1992 Q1" ~ "2006 Q4")
# Fit the models
beer_fit <- train |>
  model(
    Mean = MEAN(Beer),
    `Naïve` = NAIVE(Beer),
    `Seasonal naïve` = SNAIVE(Beer)
  )

Using residuals in R

• After estimating a model(), apply augment() to it.
• After applying augment():

augment(beer_fit)

# A tsibble: 180 x 6 [1Q]
# Key:       .model [3]
   .model Quarter  Beer .fitted .resid .innov
   <chr>    <qtr> <dbl>   <dbl>  <dbl>  <dbl>
 1 Mean   1992 Q1   443    436.   6.55   6.55
 2 Mean   1992 Q2   410    436. -26.4  -26.4 
 3 Mean   1992 Q3   420    436. -16.4  -16.4 
 4 Mean   1992 Q4   532    436.  95.6   95.6 
 5 Mean   1993 Q1   433    436.  -3.45  -3.45
 6 Mean   1993 Q2   421    436. -15.4  -15.4 
 7 Mean   1993 Q3   410    436. -26.4  -26.4 
 8 Mean   1993 Q4   512    436.  75.6   75.6 
 9 Mean   1994 Q1   449    436.  12.6   12.6 
10 Mean   1994 Q2   381    436. -55.4  -55.4 
# ℹ 170 more rows

Innovation residual properties

Innovation residuals should… - be uncorrelated - have zero mean - be homoskedastic - be Normally distributed

Example: Google closing stock prices

• Innovation residual for a naive forecast?

Example: Google closing stock prices

• Innovation residual for a naive forecast?
  • \(e_{t} = y_{t} - \hat{y}_{t} = y_{t} - y_{t-1}\).

Example: Google closing stock prices

• Innovation residual for a naive forecast?
  • \(e_{t} = y_{t} - \hat{y}_{t} = y_{t} - y_{t-1}\).
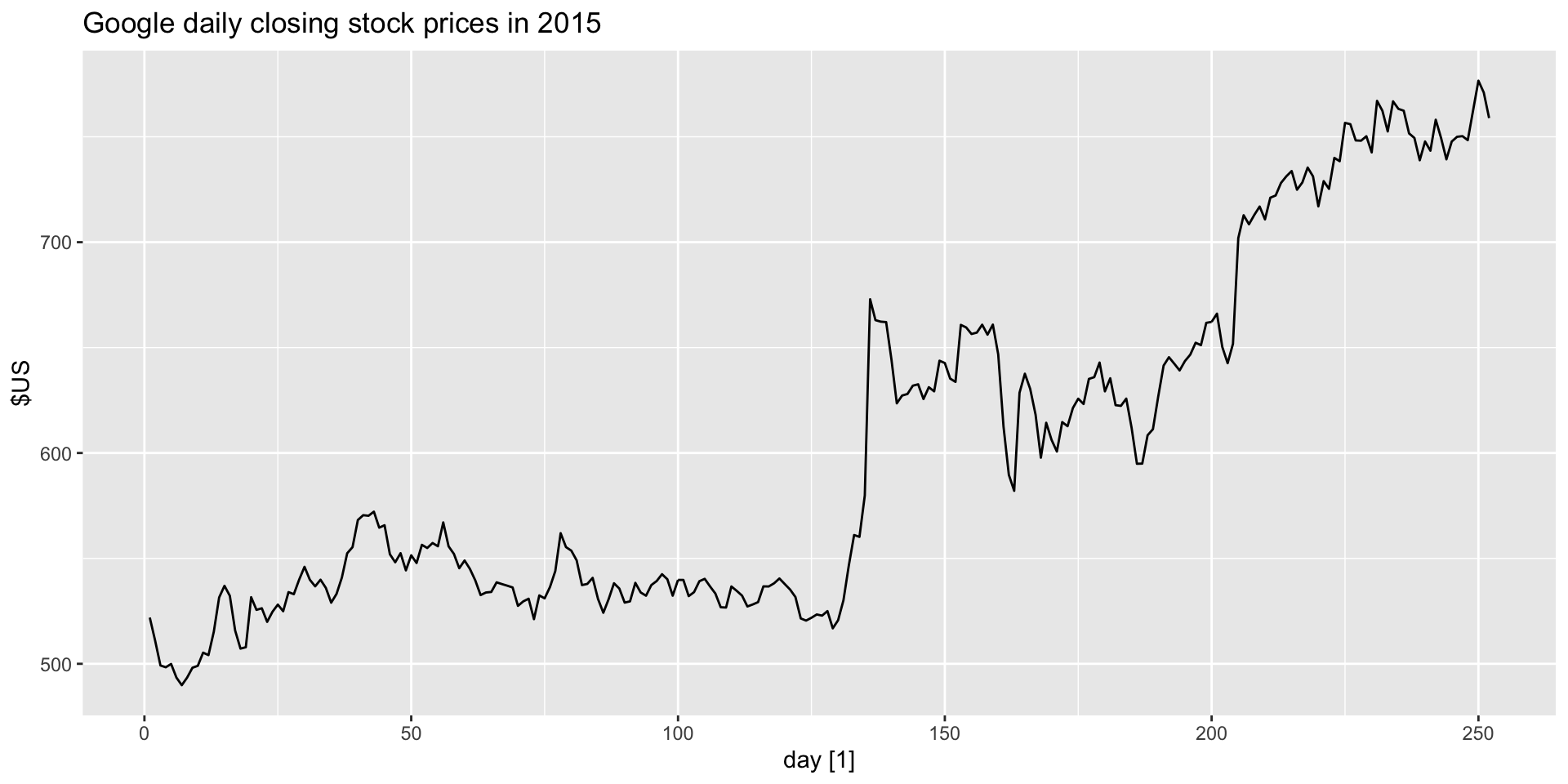
• Let’s focus on 2015:

# Re-index to trading days
google_stock <- gafa_stock |>
  filter(Symbol == "GOOG", year(Date) >= 2015) |>
  mutate(day = row_number()) |>
  update_tsibble(index = day, regular = TRUE)
# Filter the year of interest
google_2015 <- google_stock |> filter(year(Date) == 2015)

Example: Google closing stock prices

• Innovation residual for a naive forecast?
  • \(e_{t} = y_{t} - \hat{y}_{t} = y_{t} - y_{t-1}\).
• And make an autoplot:

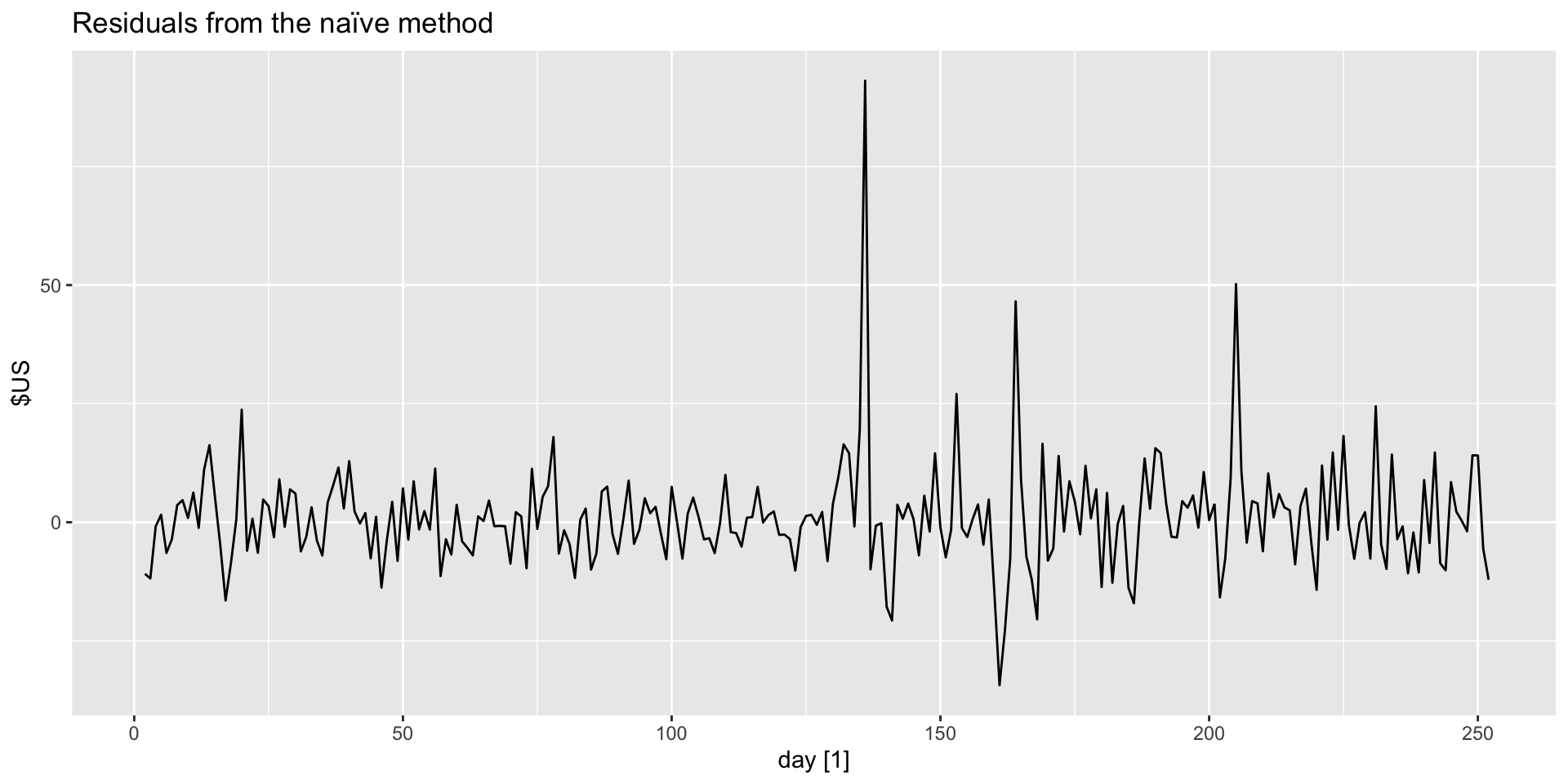
Example: Google closing stock prices residual autoplot

• Autoplot the innovation residuals:

Example: Google closing stock prices residual autoplot

• Autoplot the innovation residuals:

aug <- google_2015 |>
  model(NAIVE(Close)) |>
  augment()
autoplot(aug, .innov) +
  labs(y = "$US",
       title = "Residuals from the naïve method")

Example: Google closing stock prices residual histogram

-Produce a histogram of the innovation residuals:

Example: Google closing stock prices residual histogram

-Produce a histogram of the innovation residuals:

aug |>
  ggplot(aes(x = .innov)) +
  geom_histogram() +
  labs(title = "Histogram of residuals")

Example: Google closing stock prices ACF plot

• Produce an ACF plot:

Example: Google closing stock prices ACF plot

• Produce an ACF plot:

aug |>
  ACF(.innov) |>
  autoplot() +
  labs(title = "Residuals from the naïve method")

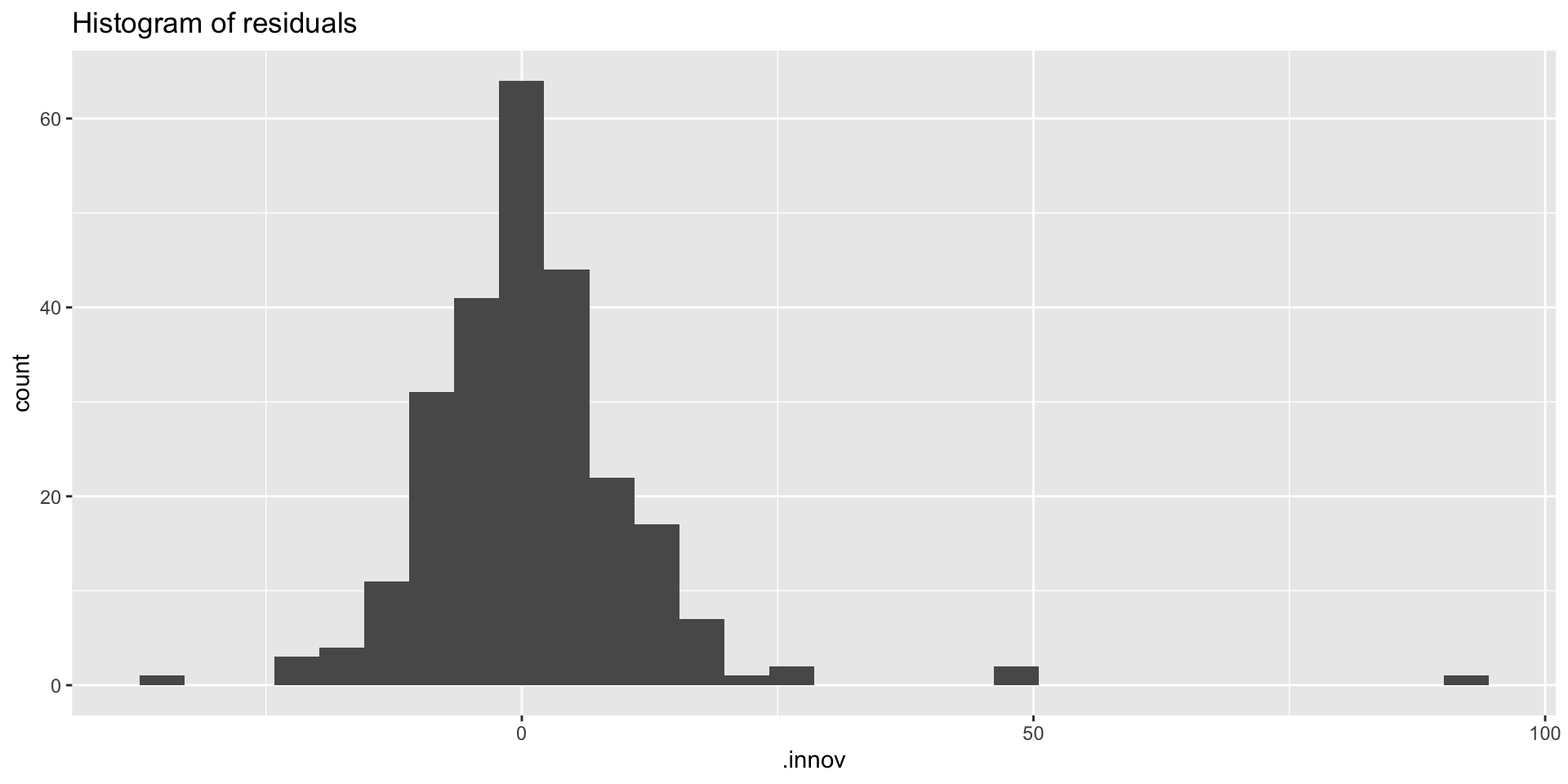
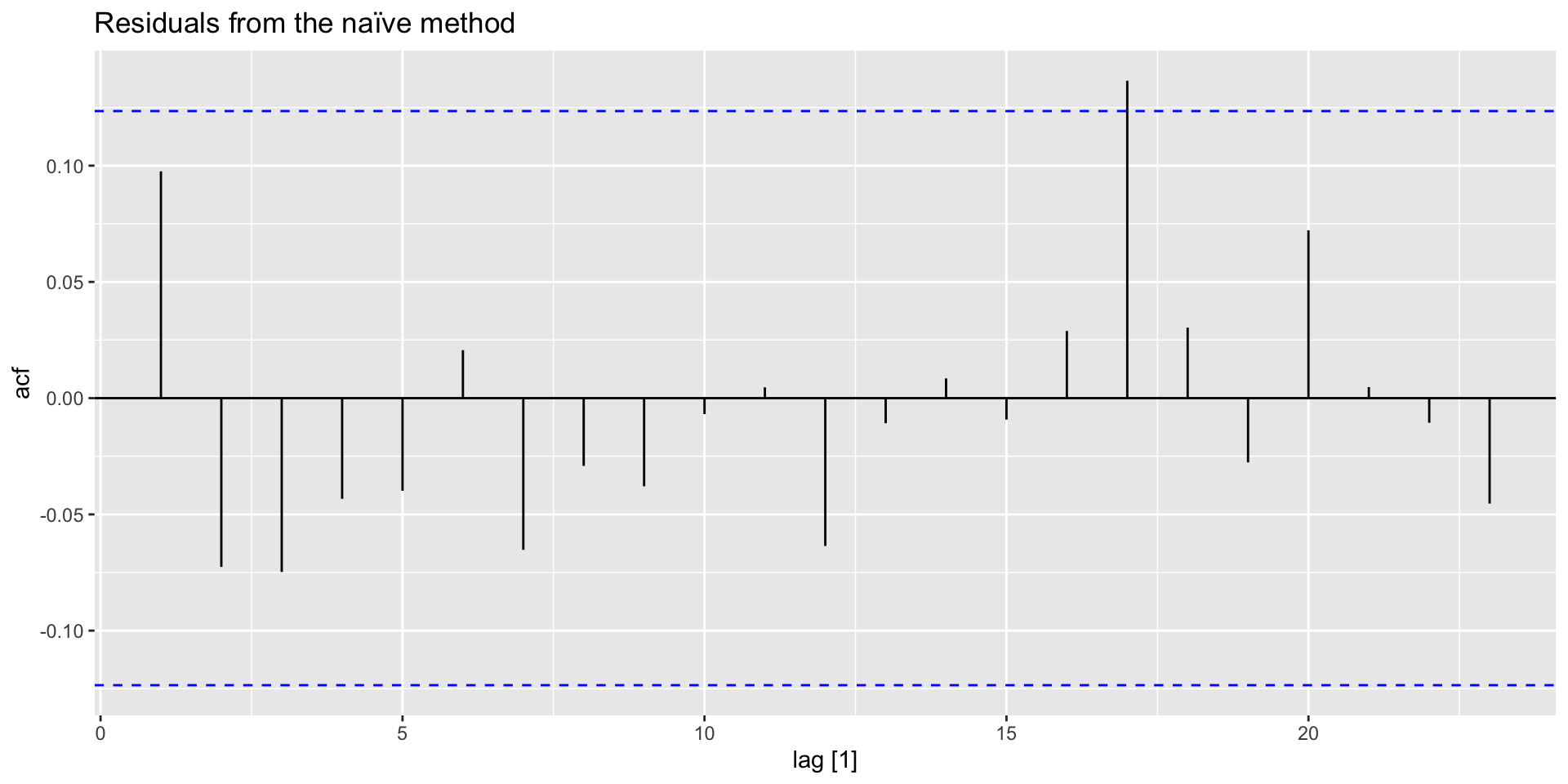
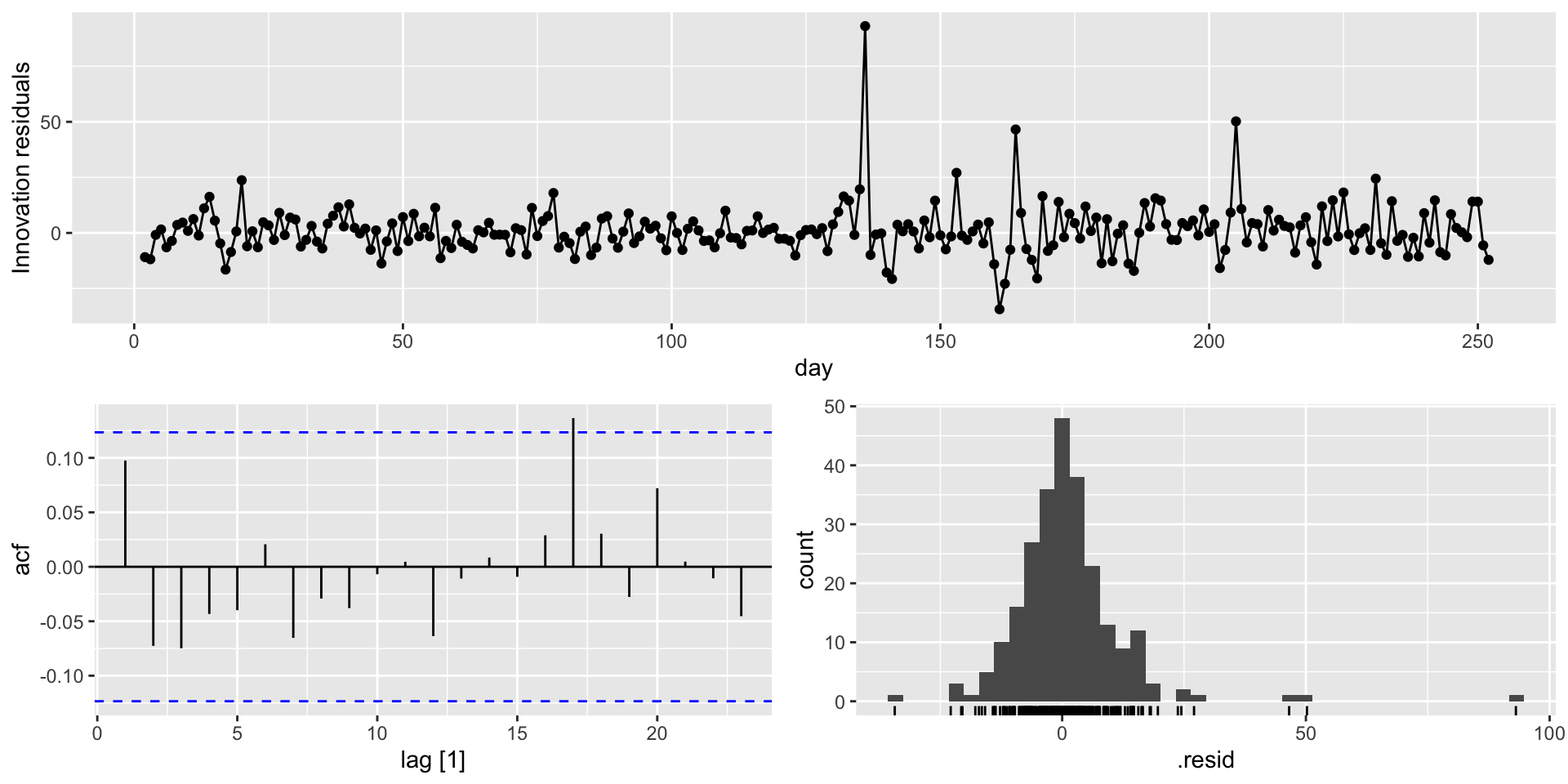
Example: Google closing stock prices tsresiduals()

• You can use tsresiduals() to produce all of these:

google_2015 |>
  model(NAIVE(Close)) |>
  gg_tsresiduals()

Example: Google closing stock prices tsresiduals()

• You can use tsresiduals() to produce all of these:

Portmanteau tests

• Recall the Box-Pierce statistic: \[ Q = T \sum_{k=1}^{l} r_{k}^{2} \]

Portmanteau tests

• Recall the Box-Pierce statistic: \[ Q = T \sum_{k=1}^{l} r_{k}^{2} \] and the Ljung-Box statistic: \[ Q^{*} = T(T+2) \sum_{k=1}^{l} \frac{r_{k}^{2}}{T-k} \]

Portmanteau tests

• Recall the Box-Pierce statistic: \[ Q = T \sum_{k=1}^{l} r_{k}^{2} \] and the Ljung-Box statistic: \[ Q^{*} = T(T+2) \sum_{k=1}^{l} \frac{r_{k}^{2}}{T-k} \] ## Portmanteau tests
• We can implement tests based on these statistics using the box_pierce and ljung_box options in features().
  • In the following, lag= \(l\).

aug |> features(.innov, box_pierce, lag = 10)

# A tibble: 1 × 4
  Symbol .model       bp_stat bp_pvalue
  <chr>  <chr>          <dbl>     <dbl>
1 GOOG   NAIVE(Close)    7.74     0.654

aug |> features(.innov, ljung_box, lag = 10)

# A tibble: 1 × 4
  Symbol .model       lb_stat lb_pvalue
  <chr>  <chr>          <dbl>     <dbl>
1 GOOG   NAIVE(Close)    7.91     0.637