Forecasting tools
BUS 323 Forecasting and Risk Analysis
Forecasting workflow
- Tidy
- Model-building
- Visualize
- Specify model
- Estimate model
- Evaluate model
- Repeat as necessary
- Forecast
Visualize
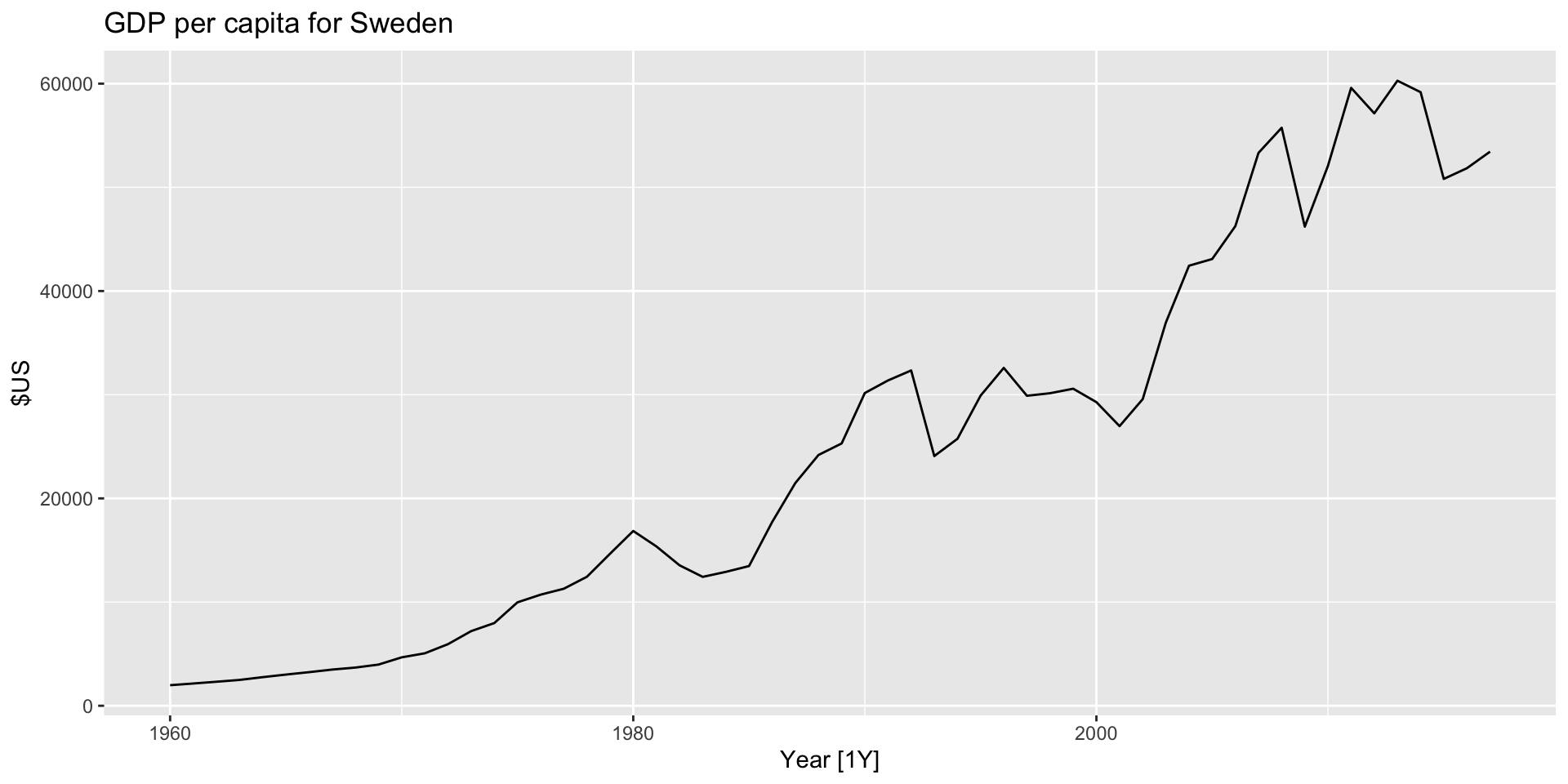
- Let’s plot Swedish GDP per capita from the
global_economydataset.
Visualize
- Let’s plot Swedish GDP per capita from the
global_economydataset.
Specify a model
- Linear trend:
Estimate the model
- To estimate the model, just specify the data you want to use:
Estimate the model
Evaluate the model
- Important to check how well your model has performed. More in a bit.
Forecast
- Use
forecast()! - To specify a timeframe for your forecast, use the
hoption:
# A fable: 789 x 5 [1Y]
# Key: Country, .model [263]
Country .model Year
<fct> <chr> <dbl>
1 Afghanistan trend_model 2018
2 Afghanistan trend_model 2019
3 Afghanistan trend_model 2020
4 Albania trend_model 2018
5 Albania trend_model 2019
6 Albania trend_model 2020
7 Algeria trend_model 2018
8 Algeria trend_model 2019
9 Algeria trend_model 2020
10 American Samoa trend_model 2018
# ℹ 779 more rows
# ℹ 2 more variables: GDP_per_capita <dist>, .mean <dbl>Forecast
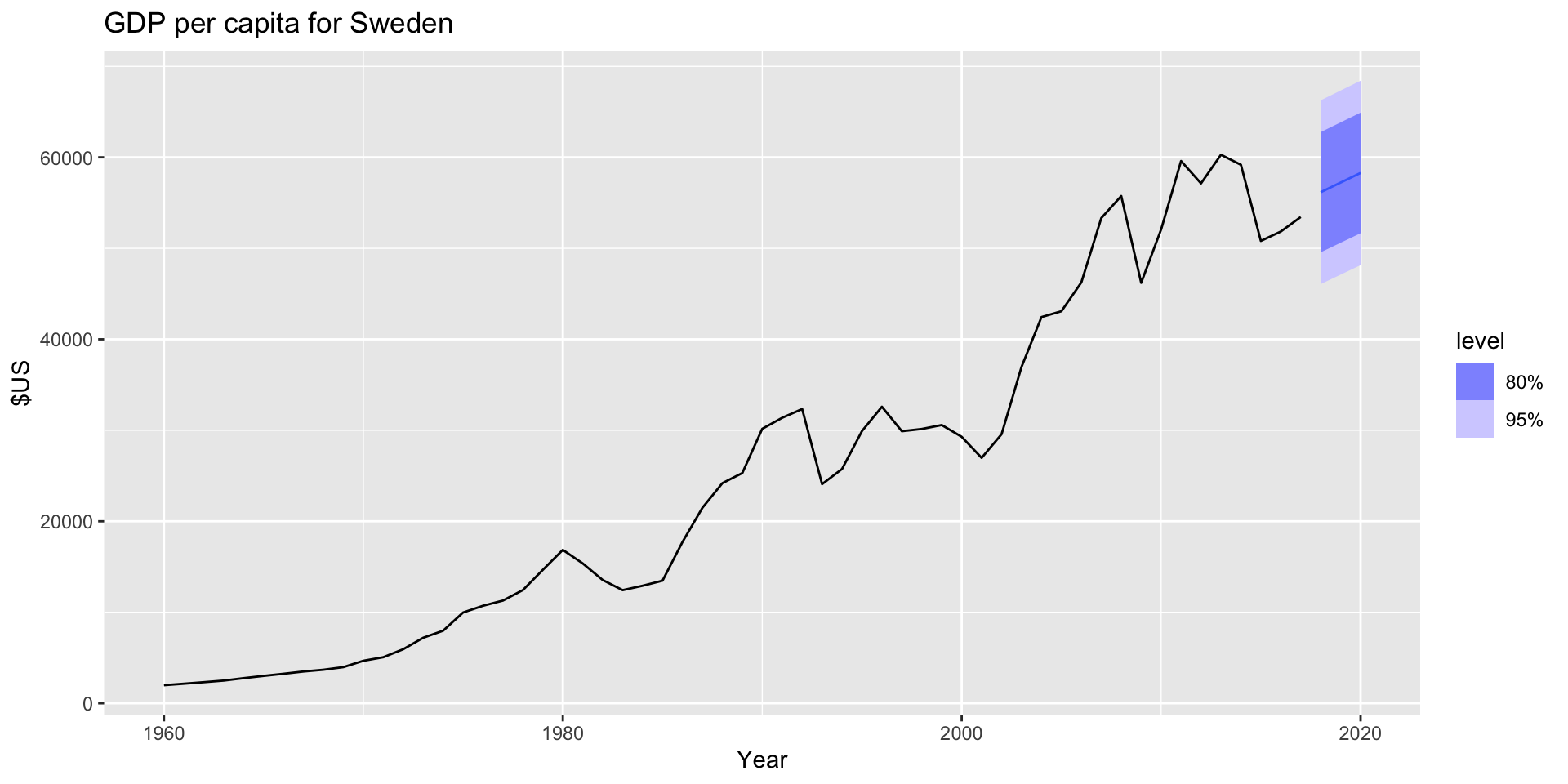
- The result is a “fable”, a forecast table. Each row corresponds to one forecast period. The
.meancolumn gives the average of the forecast distribution. - Plotting Sweden’s forecast:
Forecast
- The result is a “fable”, a forecast table. Each row corresponds to one forecast period. The
.meancolumn gives the average of the forecast distribution. - Plotting Sweden’s forecast:
More forecasting methods
- So far we have only talked about using regression to produce forecasts.
- Next we’ll dicsuss a few more simple forecasting methods.
Example dataset
- Use Australian clay brick production between 1970 and 2004 as example:
# A tsibble: 218 x 7 [1Q]
Quarter Beer Tobacco Bricks Cement Electricity Gas
<qtr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1956 Q1 284 5225 189 465 3923 5
2 1956 Q2 213 5178 204 532 4436 6
3 1956 Q3 227 5297 208 561 4806 7
4 1956 Q4 308 5681 197 570 4418 6
5 1957 Q1 262 5577 187 529 4339 5
6 1957 Q2 228 5651 214 604 4811 7
7 1957 Q3 236 5317 227 603 5259 7
8 1957 Q4 320 6152 222 582 4735 6
9 1958 Q1 272 5758 199 554 4608 5
10 1958 Q2 233 5641 229 620 5196 7
# ℹ 208 more rowsExample dataset
- Use
filter_index()to specify a range of the index to filter by:
# A tsibble: 140 x 7 [1Q]
Quarter Beer Tobacco Bricks Cement Electricity Gas
<qtr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1970 Q1 387 6807 386 1049 12328 12
2 1970 Q2 357 7612 428 1134 14493 18
3 1970 Q3 374 7862 434 1229 15664 23
4 1970 Q4 466 7126 417 1188 13781 20
5 1971 Q1 410 7255 385 1058 13299 19
6 1971 Q2 370 8076 433 1209 15230 23
7 1971 Q3 379 8405 453 1199 16667 28
8 1971 Q4 487 7974 436 1253 14484 24
9 1972 Q1 419 6500 399 1070 13838 24
10 1972 Q2 378 7119 461 1282 15919 34
# ℹ 130 more rowsExample dataset
- Use
select()to restrict attention only toBricks:
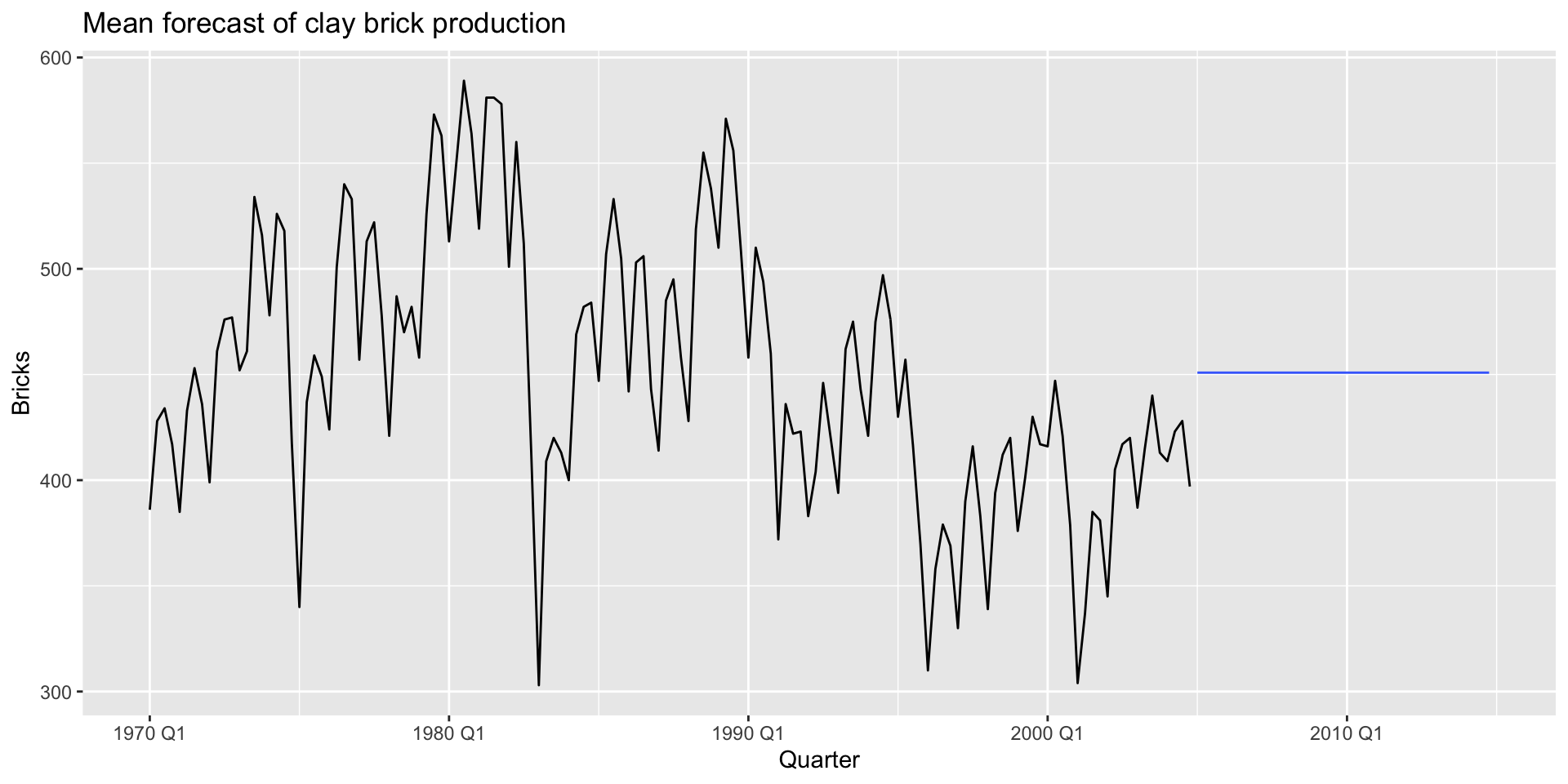
Mean method
- Use the mean of the historical data to forecast forward.
- The forecast estimate for a time series \(y\) \(h\) periods beyond the final observed period \(T\): \[ \hat{y}_{T+h|T} = \bar{y} = \frac{(y_{1} + ... + y_{t})}{T} \]
Mean method
- The function
model(MEAN())allows us to implement the mean method easily:
Mean method: forecasting
- The function
model(MEAN())allows us to implement the mean method easily:
Mean method: plotting
Mean method: plotting
Naïve method
- Use value of last observation: \[ \hat{y}_{T+h | T} = y_{T} \]
Naïve method
- Use value of last observation: \[ \hat{y}_{T+h | T} = y_{T} \]
- AKA random walk forecasts.
Naïve implementation
- Implement with
model(NAIVE()):
Naïve forecast
- Implement with
model(NAIVE()):
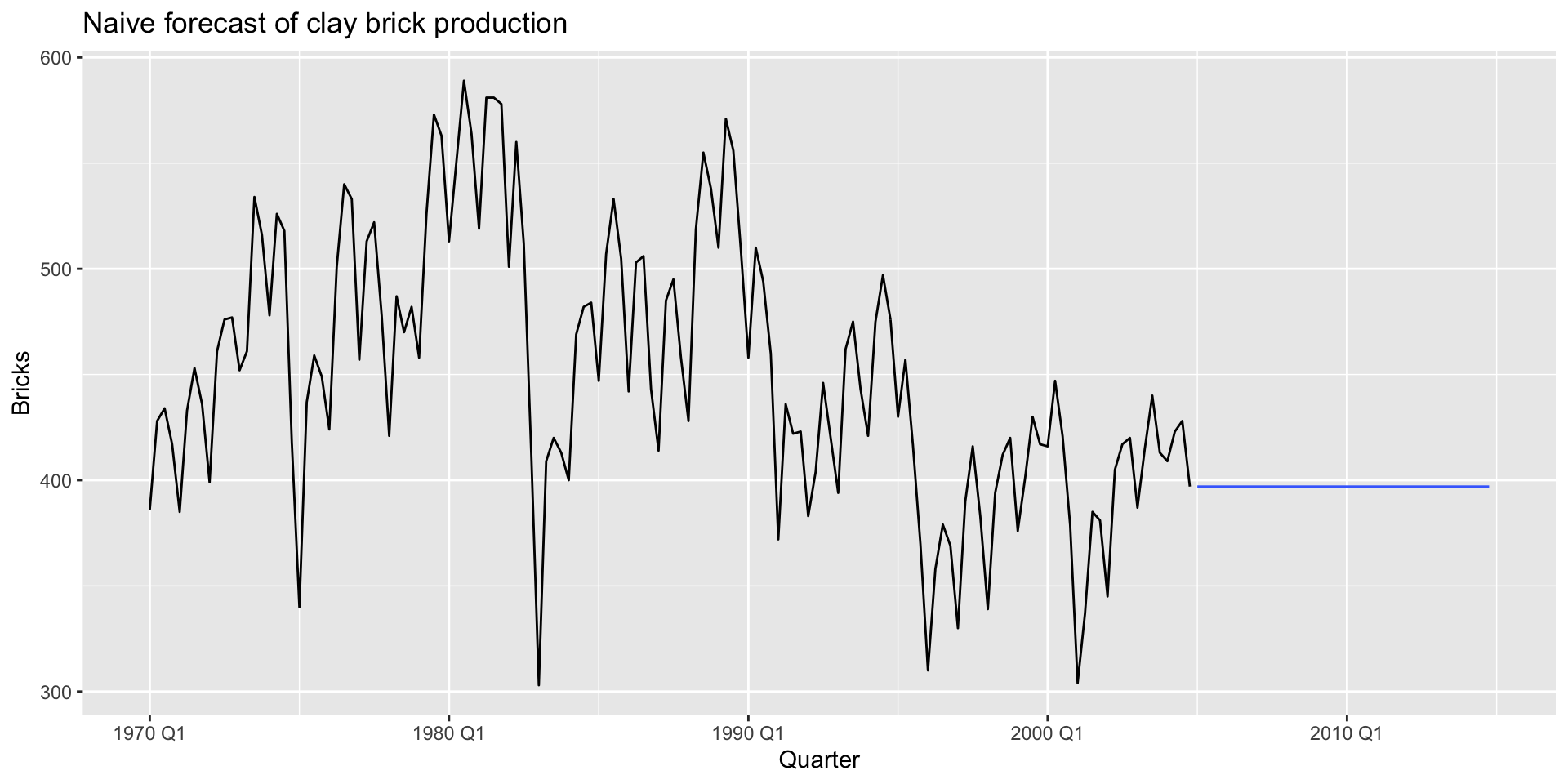
Naïve plotting
- Implement with
model(NAIVE()):
Naïve plotting
- Implement with
model(NAIVE()):
Seasonal naïve method
- Use value of last within-season observation: \[
\hat{y}_{T+h | T} = y_{T+h-m(k+1)}
\]
- \(m\): seasonal period
- \(k\): number of years in forecast prior to \(T+h\)
Seasonal naïve implementation
- Implement with
model(SNAIVE()):
Seasonal naïve forecast
# A fable: 40 x 4 [1Q]
# Key: .model [1]
.model Quarter
<chr> <qtr>
1 "SNAIVE(Bricks ~ lag(\"year\"))" 2005 Q1
2 "SNAIVE(Bricks ~ lag(\"year\"))" 2005 Q2
3 "SNAIVE(Bricks ~ lag(\"year\"))" 2005 Q3
4 "SNAIVE(Bricks ~ lag(\"year\"))" 2005 Q4
5 "SNAIVE(Bricks ~ lag(\"year\"))" 2006 Q1
6 "SNAIVE(Bricks ~ lag(\"year\"))" 2006 Q2
7 "SNAIVE(Bricks ~ lag(\"year\"))" 2006 Q3
8 "SNAIVE(Bricks ~ lag(\"year\"))" 2006 Q4
9 "SNAIVE(Bricks ~ lag(\"year\"))" 2007 Q1
10 "SNAIVE(Bricks ~ lag(\"year\"))" 2007 Q2
# ℹ 30 more rows
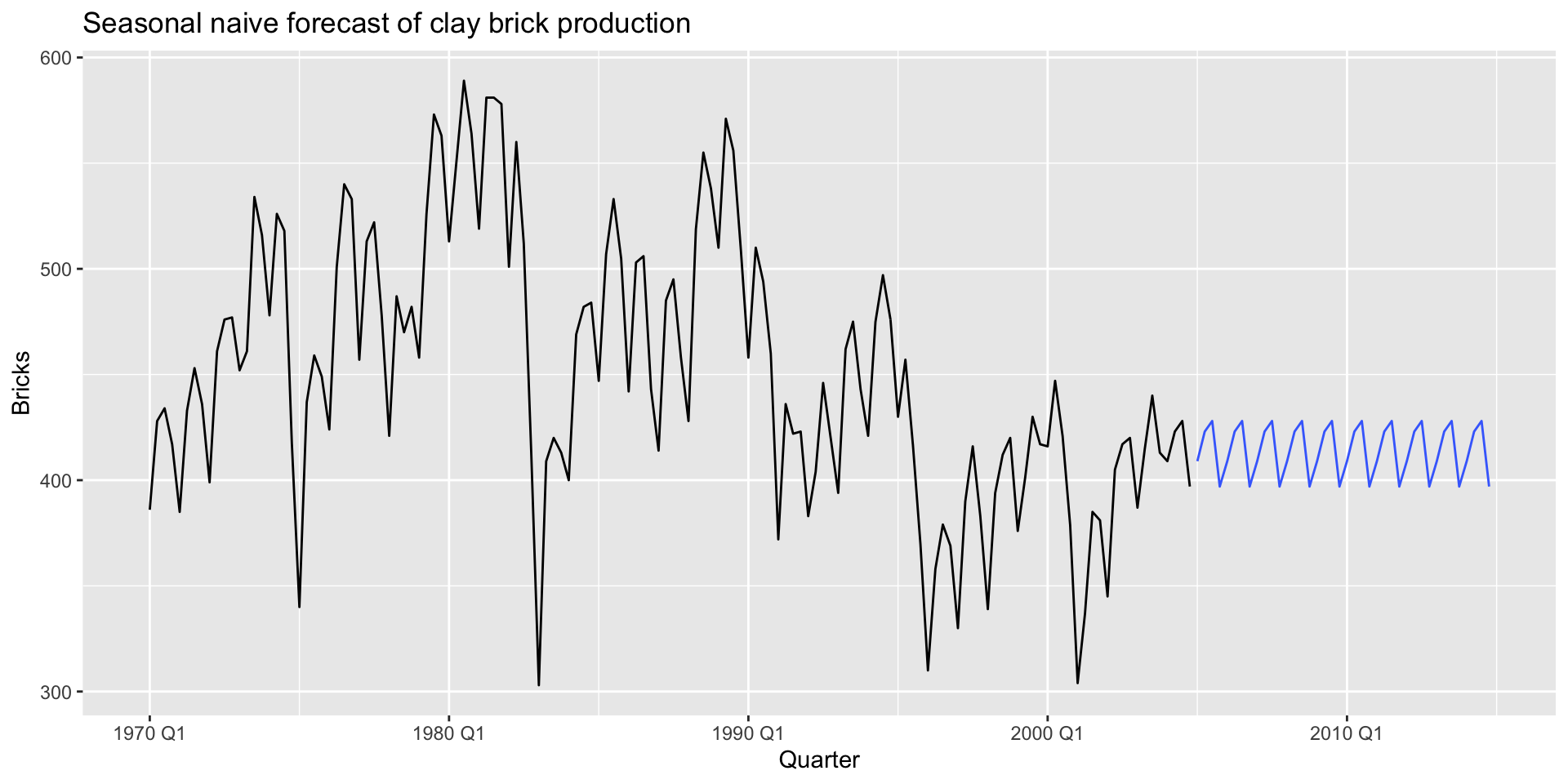
# ℹ 2 more variables: Bricks <dist>, .mean <dbl>Seasonal naïve plotting
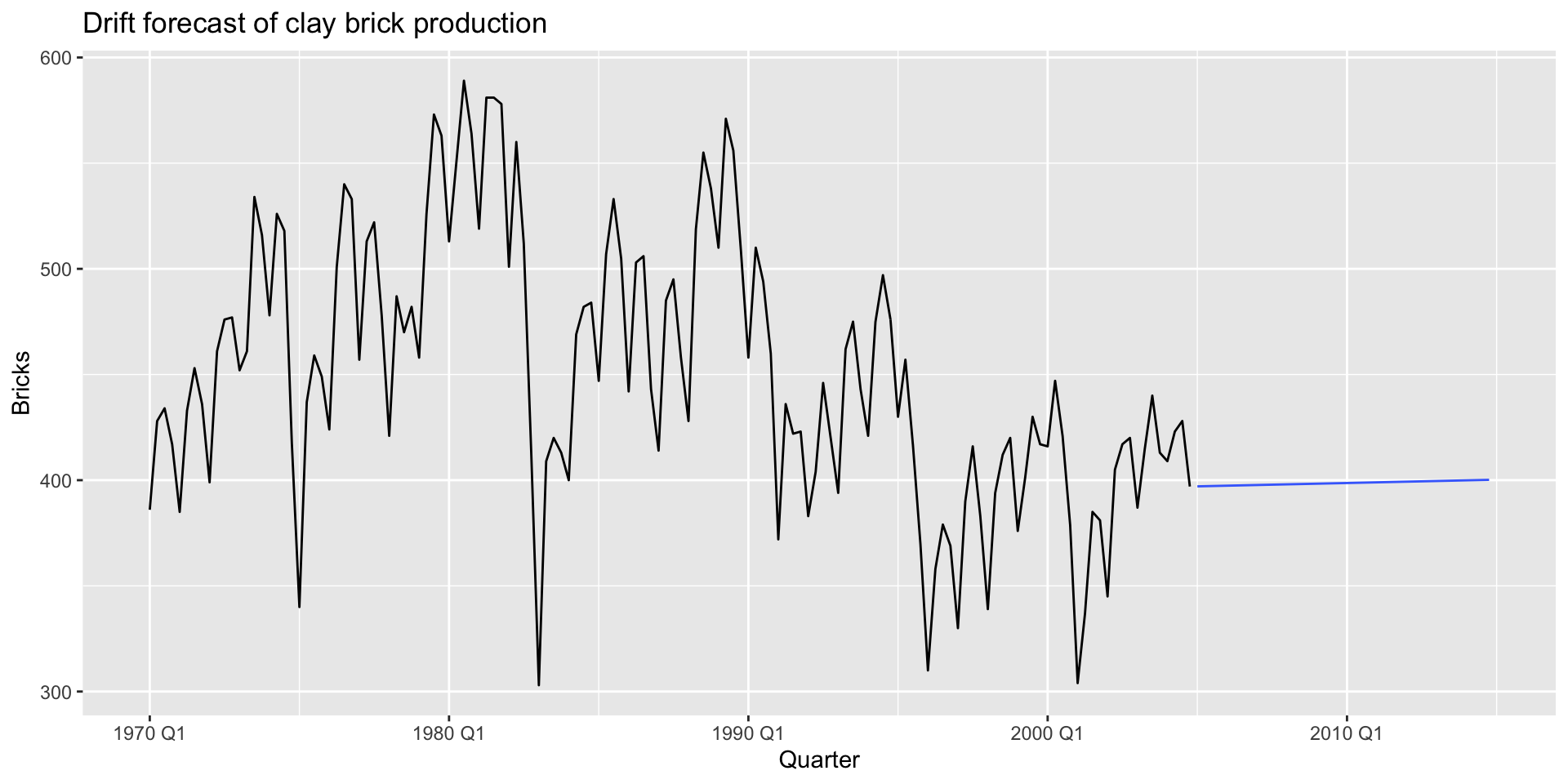
Drift method
- Naïve method allowing for “drift”
Drift method
- Naïve method allowing for “drift”
- Increase/decrease in forecast over time
Drift method
- Naïve method allowing for “drift”
- Increase/decrease in forecast over time
- Drift set to average observed change
Drift method
- Naïve method allowing for “drift”
- Increase/decrease in forecast over time
- Drift set to average observed change
- Forecast for \(T+h\): \[ \hat{y}_{T+h | T} = y_{T} + h\frac{\sum_{t=2}^{T} (y_{t} - y_{t-1})}{T-2} = y_{T} + h(\frac{y_{T}-y_{1}}{T-1}) \]
Drift implementation
- Use
model(RW()):
Drift forecast
# A fable: 40 x 4 [1Q]
# Key: .model [1]
.model Quarter
<chr> <qtr>
1 RW(Bricks ~ drift()) 2005 Q1
2 RW(Bricks ~ drift()) 2005 Q2
3 RW(Bricks ~ drift()) 2005 Q3
4 RW(Bricks ~ drift()) 2005 Q4
5 RW(Bricks ~ drift()) 2006 Q1
6 RW(Bricks ~ drift()) 2006 Q2
7 RW(Bricks ~ drift()) 2006 Q3
8 RW(Bricks ~ drift()) 2006 Q4
9 RW(Bricks ~ drift()) 2007 Q1
10 RW(Bricks ~ drift()) 2007 Q2
# ℹ 30 more rows
# ℹ 2 more variables: Bricks <dist>, .mean <dbl>Drift plotting
Drift plotting