Evaluating your time series regression

BUS 323 Forecasting and Risk Analysis

Residuals: assumptions

Assumed to have average of zero: \[ \sum_{t=1}^{T} e_{t} = 0 \]
Assumed to have zero correlation with regressors:

\[ \sum_{t=1}^{T} x_{k,t} e_{t} = 0 \text{ }\forall \text{ } k \].

Residuals: assumptions

It’s important to check that these assumptions hold after estimating a regression model.

Baseline regression

Recall our time series regression for the us_change dataset:

mr_c <- us_change |>
  model(TSLM(Consumption ~ Income + Production + Unemployment + Savings))
report(mr_c)

Baseline regression

Recall our time series regression for the us_change dataset:

Series: Consumption 
Model: TSLM 

Residuals:
     Min       1Q   Median       3Q      Max 
-0.90555 -0.15821 -0.03608  0.13618  1.15471 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.253105   0.034470   7.343 5.71e-12 ***
Income        0.740583   0.040115  18.461  < 2e-16 ***
Production    0.047173   0.023142   2.038   0.0429 *  
Unemployment -0.174685   0.095511  -1.829   0.0689 .  
Savings      -0.052890   0.002924 -18.088  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3102 on 193 degrees of freedom
Multiple R-squared: 0.7683, Adjusted R-squared: 0.7635
F-statistic:   160 on 4 and 193 DF, p-value: < 2.22e-16

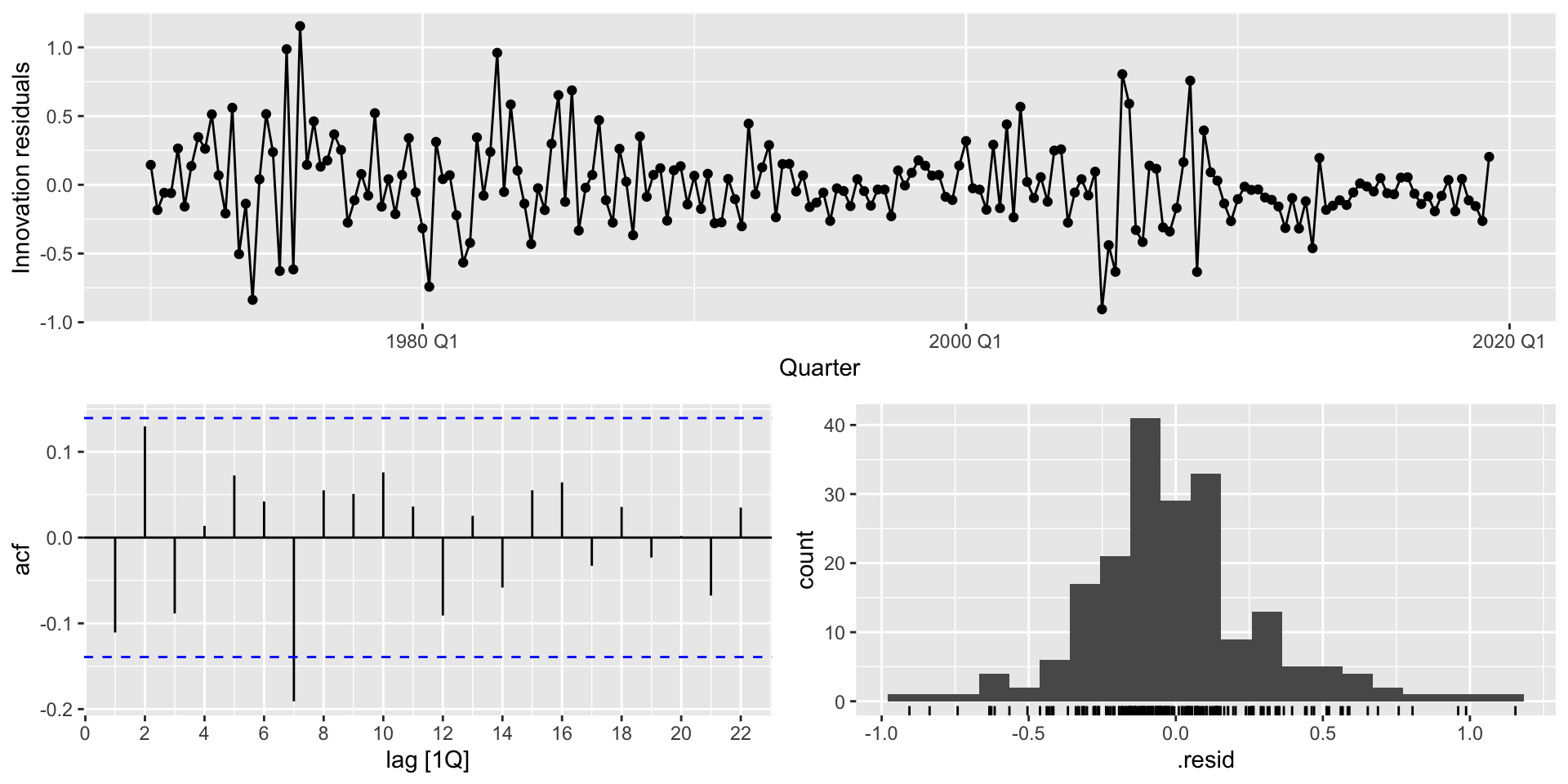
Residual plots

When you use TSLM() you can generate residual plots with gg_tsresiduals():

mr_c |>
  gg_tsresiduals()

Residual plots

When you use TSLM() you can generate residual plots with gg_tsresiduals():

Autocorrelation tests

The ACF plot is a neat visual check for autocorrelation.
Implicit single hypothesis tests in relying on it
For a joint hypothesis test, use portmanteau tests.

Box-Pierce

The Box-Pierce test is based on the following statistic: \[ Q = T \sum_{k=1}^{l} r_{k}^{2} \] where $l$ is the maximum lag under consideration; $T$ is the total number of time periods (observations, in a time series).
If all $r_{k}$ are small, $Q$ will also be small.
Rule of thumb:
- Use $l=10$ for non-seasonal data
- Use $l = \frac{T}{5}$ for seasonal data.

Hypothesis testing

Hypothesis testing proceeds as usual here. Compare $Q$ to the $\chi^{2}$ distribution critical value at your chosen level of significance.
R will give you the $p$-value associated with the hypothesis test directly, so you can just use that in practice. Compare the $p$-value to your chosen level of significance $\alpha$. If $p<\alpha$, you can reject $H_{0}$ at that level of significance.

Ljung-Box

The Ljung-Box test is more commonly used.
At higher lag values, autocorrelations tend to become noisy.
Ljung-Box adds weights to account for the noise at higher lag values.
Ljung-Box also approximates the $\chi^{2}$ distribution better than Box-Pierce: \[ Q^{*} = T(T+2) \sum_{k=1}^{l} \frac{r_{k}^{2}}{T-k} \]

Implementing Box-Pierce

To implement easily, use augment() and features():

augment(mr_c) |>
  features(.innov, box_pierce, lag = 10)

# A tibble: 1 × 3
  .model                                                       bp_stat bp_pvalue
  <chr>                                                          <dbl>     <dbl>
1 TSLM(Consumption ~ Income + Production + Unemployment + Sav…    18.2    0.0518

Implementing Ljung-Box

Similar set-up for Ljung-Box:

augment(mr_c) |>
  features(.innov, ljunbg_box, lag = 10)

# A tibble: 1 × 3
  .model                                                       lb_stat lb_pvalue
  <chr>                                                          <dbl>     <dbl>
1 TSLM(Consumption ~ Income + Production + Unemployment + Sav…    18.9    0.0420

Checking the zero conditional mean assumption

One of the Gauss-Markov assumptions underlying regression estimation via OLS is \[ E(e | X) = 0. \]
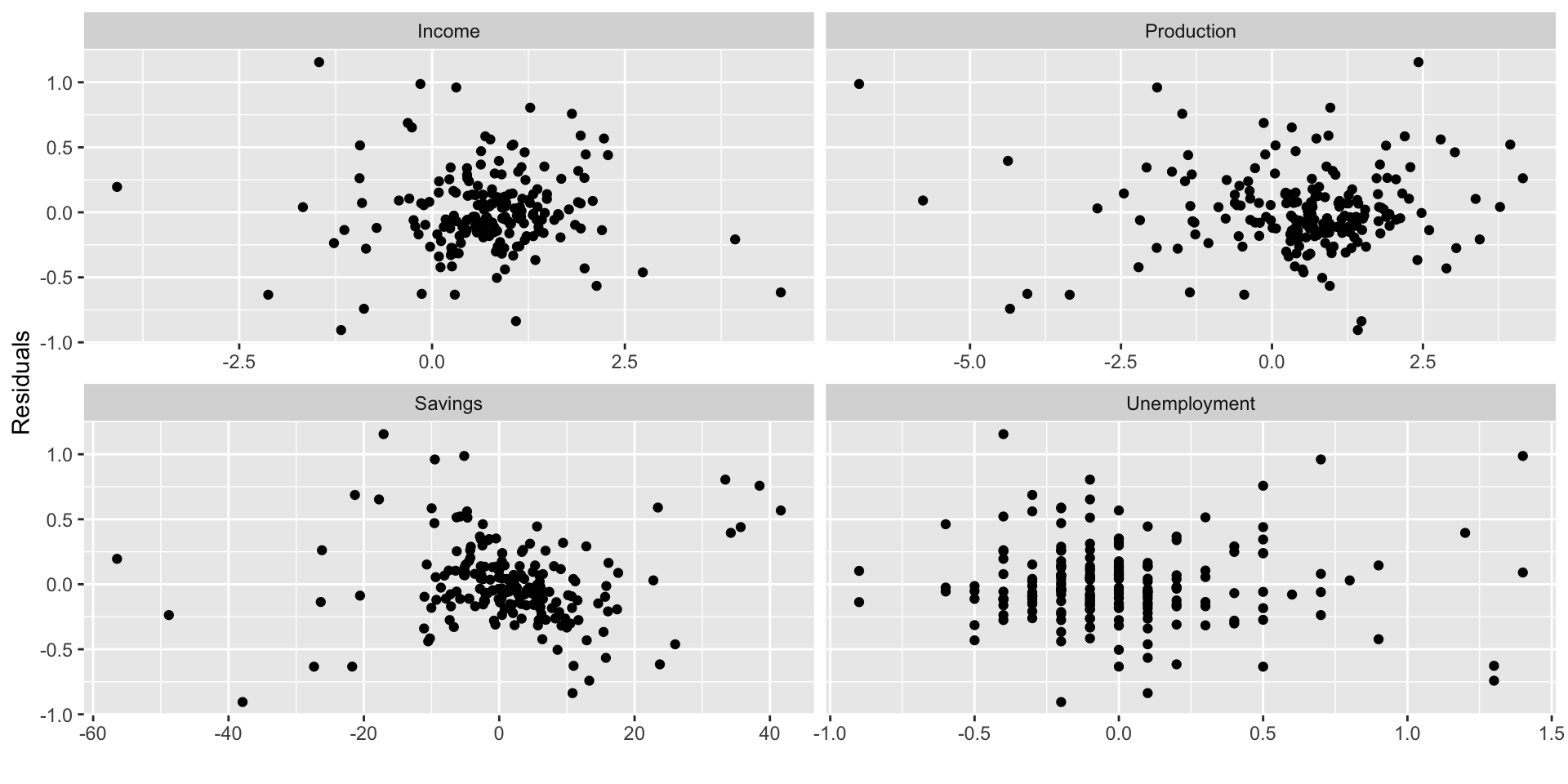
We can check how well our regression satisfies this assumption visually by scattering the residuals against each predictor variable.
It’s not a bad idea to scatter the residuals against excluded predictor variables to make sure they aren’t relevant.

Making scatterplots

First, we’ll need to add the residuals to the us_change dataset:

us_change |>
  left_join(residuals(mr_c), by = "Quarter")

Making scatterplots

Next we’ll want to turn the variables for plotting into long form:

us_change |>
  left_join(residuals(mr_c), by = "Quarter") |>
  pivot_longer(Income:Unemployment,
               names_to = "regressor", values_to = "x")

Making scatterplots

Finally we can use facet_wrap to add four plots to one plot area:

us_change |>
  left_join(residuals(mr_c), by = "Quarter") |>
  pivot_longer(Income:Unemployment,
               names_to = "regressor", values_to = "x") |>
  ggplot(aes(x = x, y = .resid)) +
  geom_point() +
  facet_wrap(. ~ regressor, scales = "free_x") +
  labs(y = "Residuals", x = "")

Making scatterplots

Finally we can use facet_wrap to add four plots to one plot area:

Residual plots against fitted values

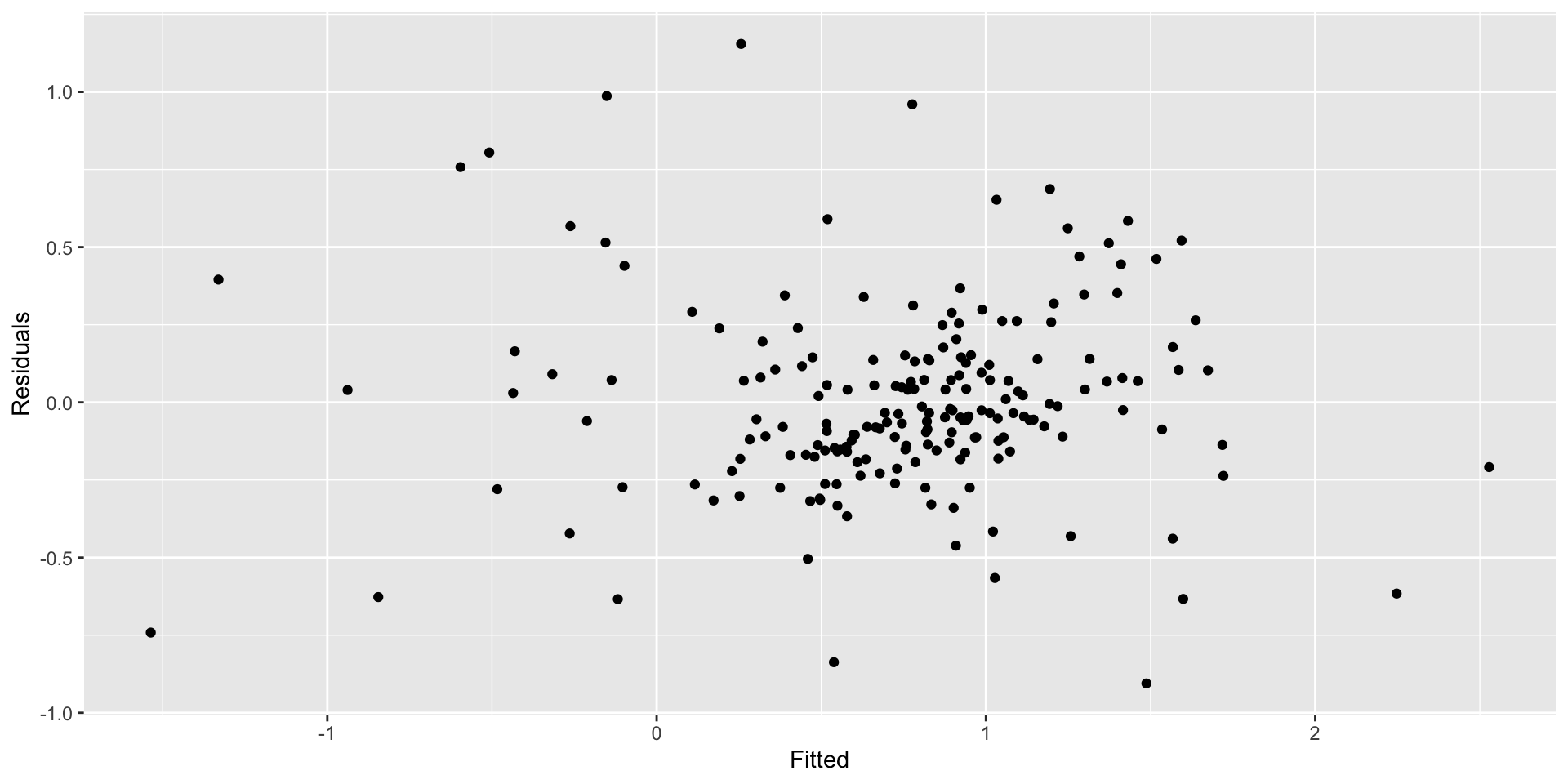
We also want to see no relationship between the residuals and the predictions from our model.
You can access the predicted (fitted) values from a time series regression object by calling it: augment(mr_c)$.fitted
You can access the residuals similarly: augment(mr_c)$.resid
Plotting is simple once you’ve got those:

augment(mr_c) |>
  ggplot(aes(x = .fitted, y = .resid)) +
  geom_point() + labs(x = "Fitted", y = "Residuals")

Residual plots against fitted values

Forecasting with regression

Recall predicted values can be obtained via \[ \hat{y}_{t} = \hat{\beta}_{0} + \hat{\beta}_{1} x_{1,t} + ... + \hat{\beta}_{k,t} \] Plugging in observed values of the regressors for a given $t$ will return the relevant prediction for $y$. But we are interested in forecasting values of $y$, for which $x$ are not observed.

Ex-ante forecasts

Ex-ante forecasts are genuine forecasts, based only on existing observations and extending beyond the period of observation. To make ex ante predictions, we’ll need forecasts of the to forecast the regressand.
- We’ll talk over some simple methods for forecasting predictors next time, then more sophisticated approaches later on.

Ex-post forecasts

Ex-post forecasts are made using observed values. So you’d define a “forecast period”, use only observations prior to that period to “train” your regression, then generate an ex-ost forecast for the forecast period.
- Ex-post forecasting is useful for testing and evaluating your model.

A couple of useful predictors

Before we do our first forecast, let’s define a couple of useful predictors that exist within a given time series and can be forecasted forward really easily.

Trend

A linear trend can be modeled by using $t$ as a predictor: \[ y_{t} = \beta_{0} + \beta_{1} t + \epsilon_{t} \]
You can add a linear trend to a TSLM() command with the trend() option.

Dummy variables

A dummy variable is one that is equal to 1 when a given condition is met and is equal to 0 otherwise.
These are useful for accounting for outliers, among other things
- e.g. If your time series of retail sales includes Labor Day, when demand might be abnormally high, you might want to include a variable that accounts for the effect of Labor Day separate from your other predictors.
If you want to account for seasonal differences with dummy variables, you can do so easily with the season() option in TSLM().

Example: beer production

recent_production <- aus_production |>
  filter(year(Quarter) >= 1992)

# A tsibble: 6 x 7 [1Q]
  Quarter  Beer Tobacco Bricks Cement Electricity   Gas
    <qtr> <dbl>   <dbl>  <dbl>  <dbl>       <dbl> <dbl>
1 1992 Q1   443    5777    383   1289       38332   117
2 1992 Q2   410    5853    404   1501       39774   151
3 1992 Q3   420    6416    446   1539       42246   175
4 1992 Q4   532    5825    420   1568       38498   129
5 1993 Q1   433    5724    394   1450       39460   116
6 1993 Q2   421    6036    462   1668       41356   149

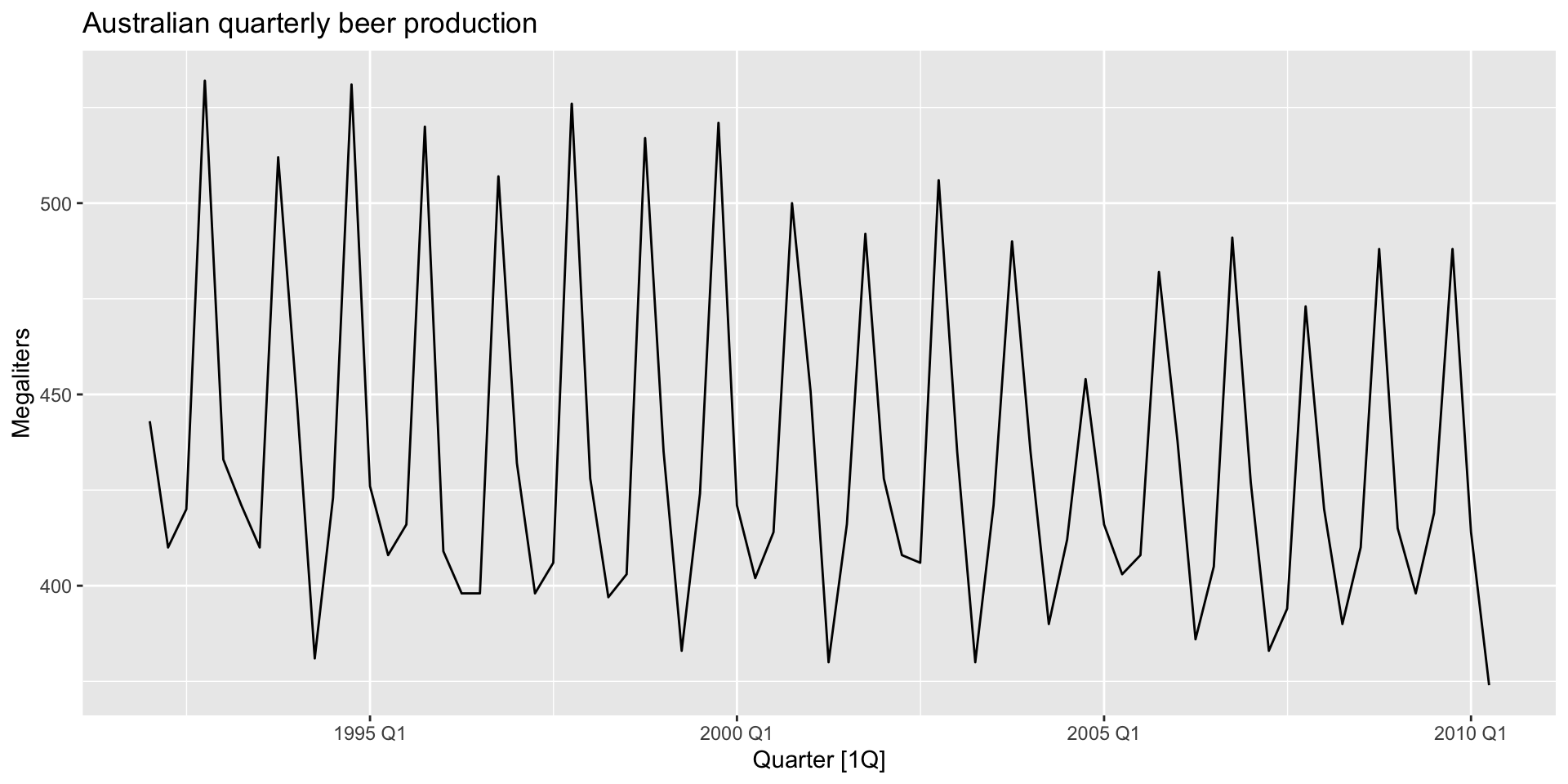
Example: beer production

Let’s estimate a model with a linear trend and seasonal dummies. Since the seasonality is quarterly, we’ll want quarter dummies: \[ y_{t} = \beta_{0} + \beta_{1} t + \beta_{2} d_{2,t} + \beta_{3} d_{3,t} + \beta_{4} d_{4,t} + \epsilon_{t} \]

Example: beer production

To implement in R:

lm_beer <- recent_production |>
  model(TSLM(Beer ~ trend() + season()))
report(lm_beer)

Series: Beer 
Model: TSLM 

Residuals:
     Min       1Q   Median       3Q      Max 
-42.9029  -7.5995  -0.4594   7.9908  21.7895 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)   441.80044    3.73353 118.333  < 2e-16 ***
trend()        -0.34027    0.06657  -5.111 2.73e-06 ***
season()year2 -34.65973    3.96832  -8.734 9.10e-13 ***
season()year3 -17.82164    4.02249  -4.430 3.45e-05 ***
season()year4  72.79641    4.02305  18.095  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 12.23 on 69 degrees of freedom
Multiple R-squared: 0.9243, Adjusted R-squared: 0.9199
F-statistic: 210.7 on 4 and 69 DF, p-value: < 2.22e-16

Example: beer production

Plot fitted values against observed values:

augment(lm_beer) |>
  ggplot(aes(x = Quarter)) +
  geom_line(aes(y = Beer, colour = "Data")) +
  geom_line(aes(y = .fitted, colour = "Fitted")) +
  scale_colour_manual(
    values = c(Data = "black", Fitted = "orange")
  ) +
  labs(y = "Megaliters",
       title = "Australian quarterly beer production") +
  guides(colour = guide_legend(title = "Series"))

Example: beer production

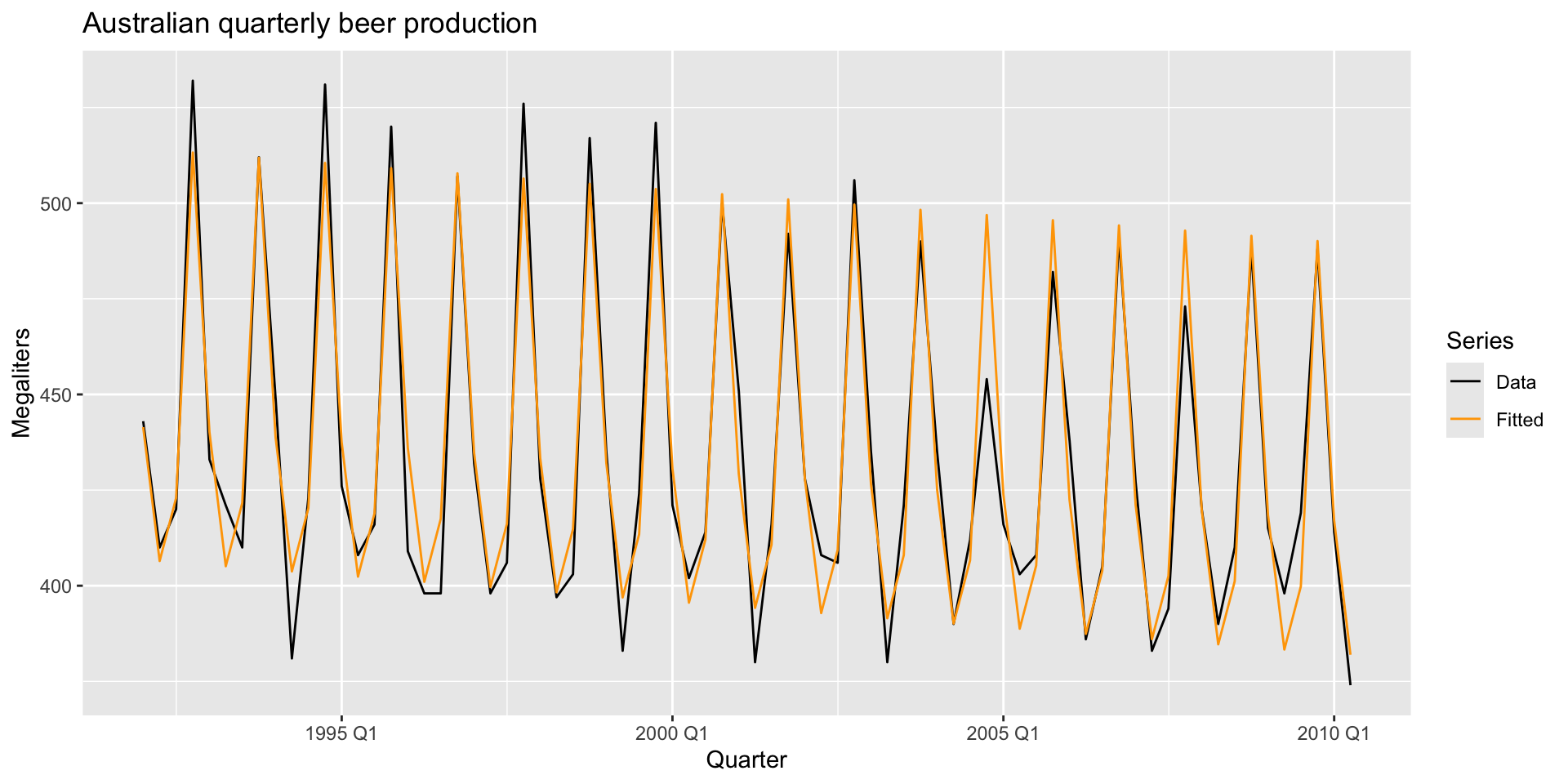
Try taking the season dummies out and see how the fit looks. Try taking the trend out and see how the fit looks.

Let’s forecast!

You can make a forecast easily if you have forecasts for the predictors pretty easily, with the forecast() function:

fc_beer <- forecast(lm_beer)
fc_beer |>
  autoplot(recent_production) +
  labs(
  title = "Beer production forecasts",
  y = "Megaliters"
  )

Let’s forecast!

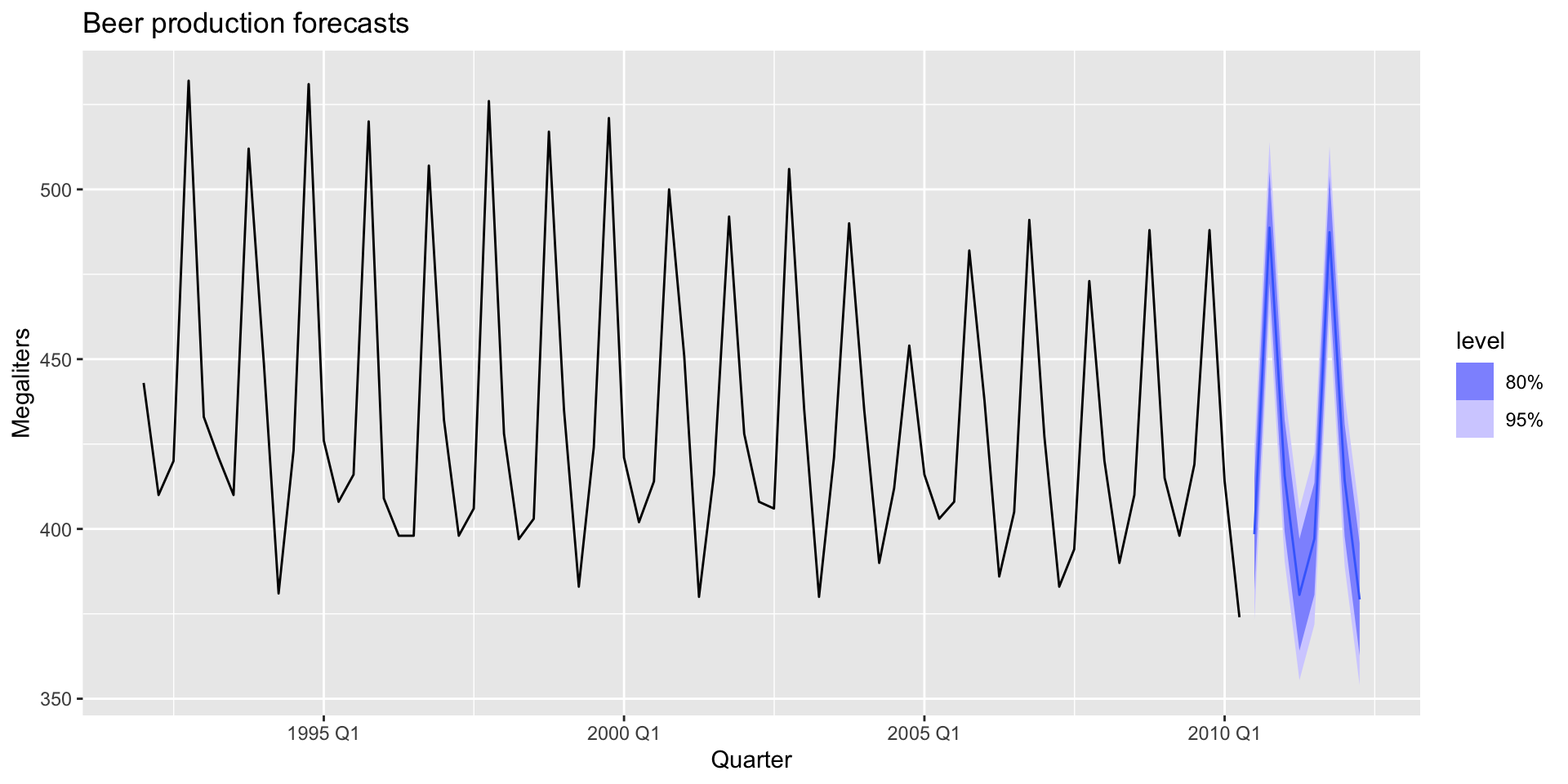
Scenario based forecasting

Suppose we want to forecast consumption change in the US under the assumption that unemployment remains constant, but income increases by 1% and savings increase by 0.5%. We’d like another scenario where income decreases by 1% andf savings decrease by 0.5%. We can use the scenarios() function to build new datasets that include our scenarios, and the new_data() function to define how far forward we’d like to forecast.
Base model:

lm_uschange <- us_change |>
  model(
    lm = TSLM(Consumption ~ Income + Savings + Unemployment)
    )

Scenario based forecasting

Building our scenarios:

future_scenarios <- scenarios(
  Increase = new_data(us_change, 4) |>
    mutate(Income=1, Savings=0.5, Unemployment=0),
  Decrease = new_data(us_change, 4) |>
    mutate(Income=-1, Savings=-0.5, Unemployment=0),
  names_to = "Scenario")

Check what these data look like now.

Scenario based forecasting

Let’s make our forecasts:

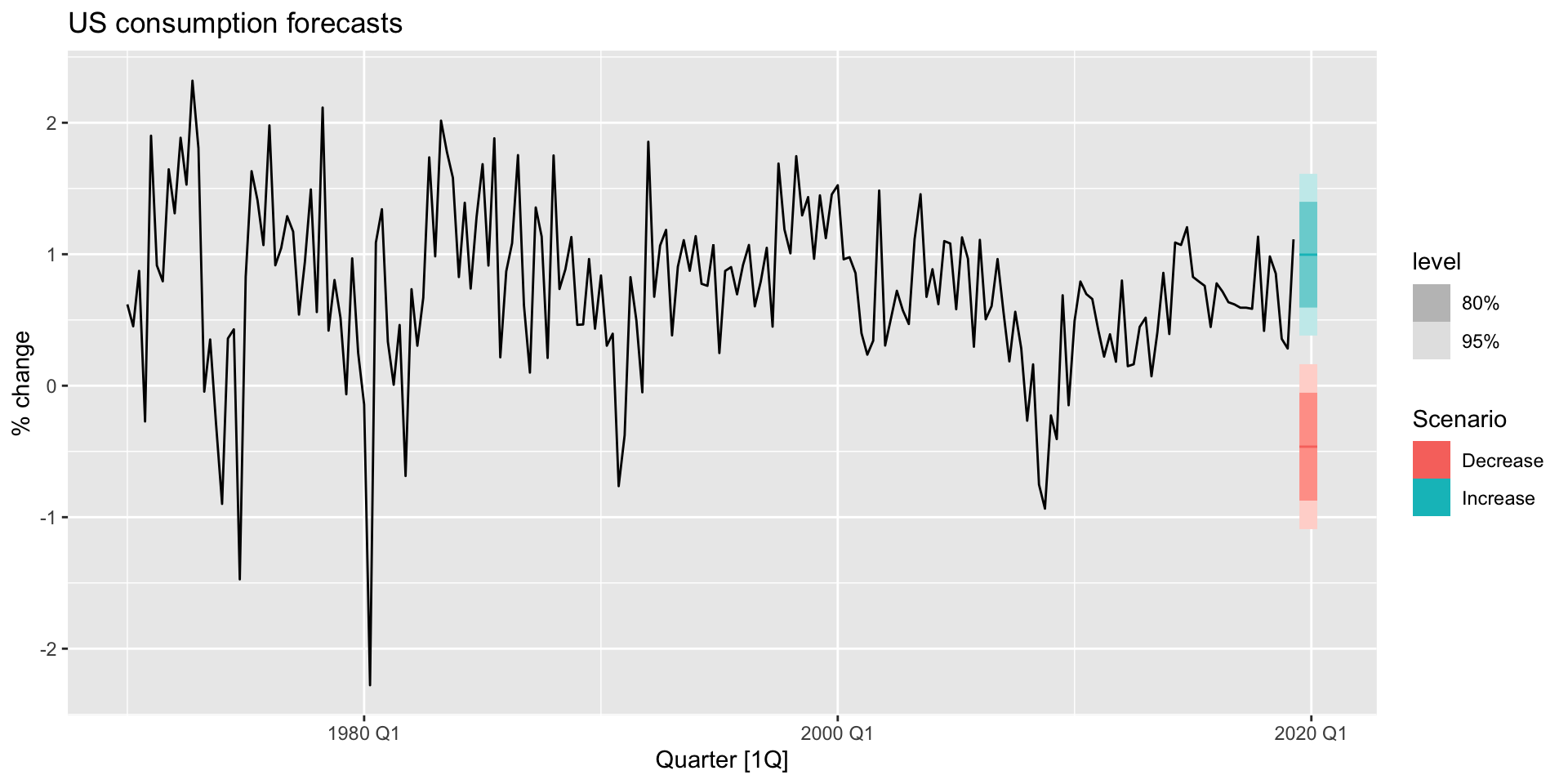
fc_uschange <- forecast(lm_uschange, new_data = future_scenarios)

Scenario based forecasting

And plot:

us_change |>
  autoplot(Consumption) +
  autolayer(fc_uschange) +
  labs(title= "US consumption forecasts", y = "% change")