# A tsibble: 6 x 6 [1Q]
Quarter Consumption Income Production Savings Unemployment
<qtr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1970 Q1 0.619 1.04 -2.45 5.30 0.9
2 1970 Q2 0.452 1.23 -0.551 7.79 0.5
3 1970 Q3 0.873 1.59 -0.359 7.40 0.5
4 1970 Q4 -0.272 -0.240 -2.19 1.17 0.700
5 1971 Q1 1.90 1.98 1.91 3.54 -0.100
6 1971 Q2 0.915 1.45 0.902 5.87 -0.100Time series regression in R
BUS 323 Forecasting and Risk Analysis
Getting set up
- We’ll work with the
us_changedataset today.
head(us_change)Plotting multiple series on a time plot
autoplotplots a single series across time.- We want to plot consumption and income change on one plot.
- To plot two, we’ll have to transform the data such that both series correspond to one variable. We can use
pivot_longer()to do so.
us_change |>
pivot_longer(c(Consumption, Income), names_to="Series")Plotting multiple series on a time plot
- Great, now we can autoplot
value
us_change |>
pivot_longer(c(Consumption, Income), names_to="Series") |>
autoplot(value) +
labs(y = "% change")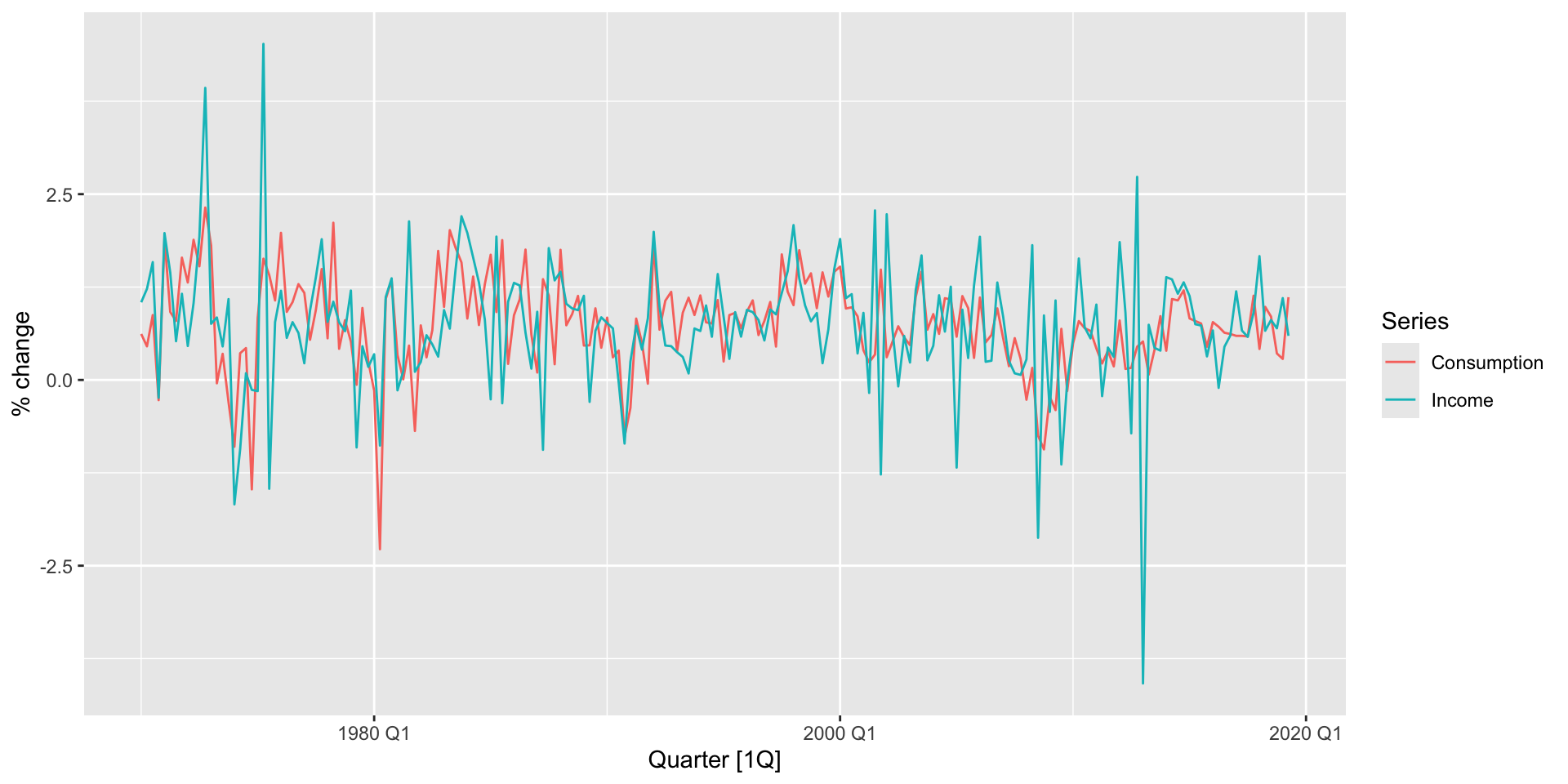
Plotting a line of best fit
- Adding a regression line to a scatterplot is simple with
geom_smoothand themethod = "lm"option:
us_change |>
ggplot(aes(x = Income, y = Consumption)) +
labs(y = "Consumption (quarterly % change)",
x = "Income (quarterly % change)") +
geom_point() +
geom_smooth(method = "lm", se = FALSE)Plotting a line of best fit
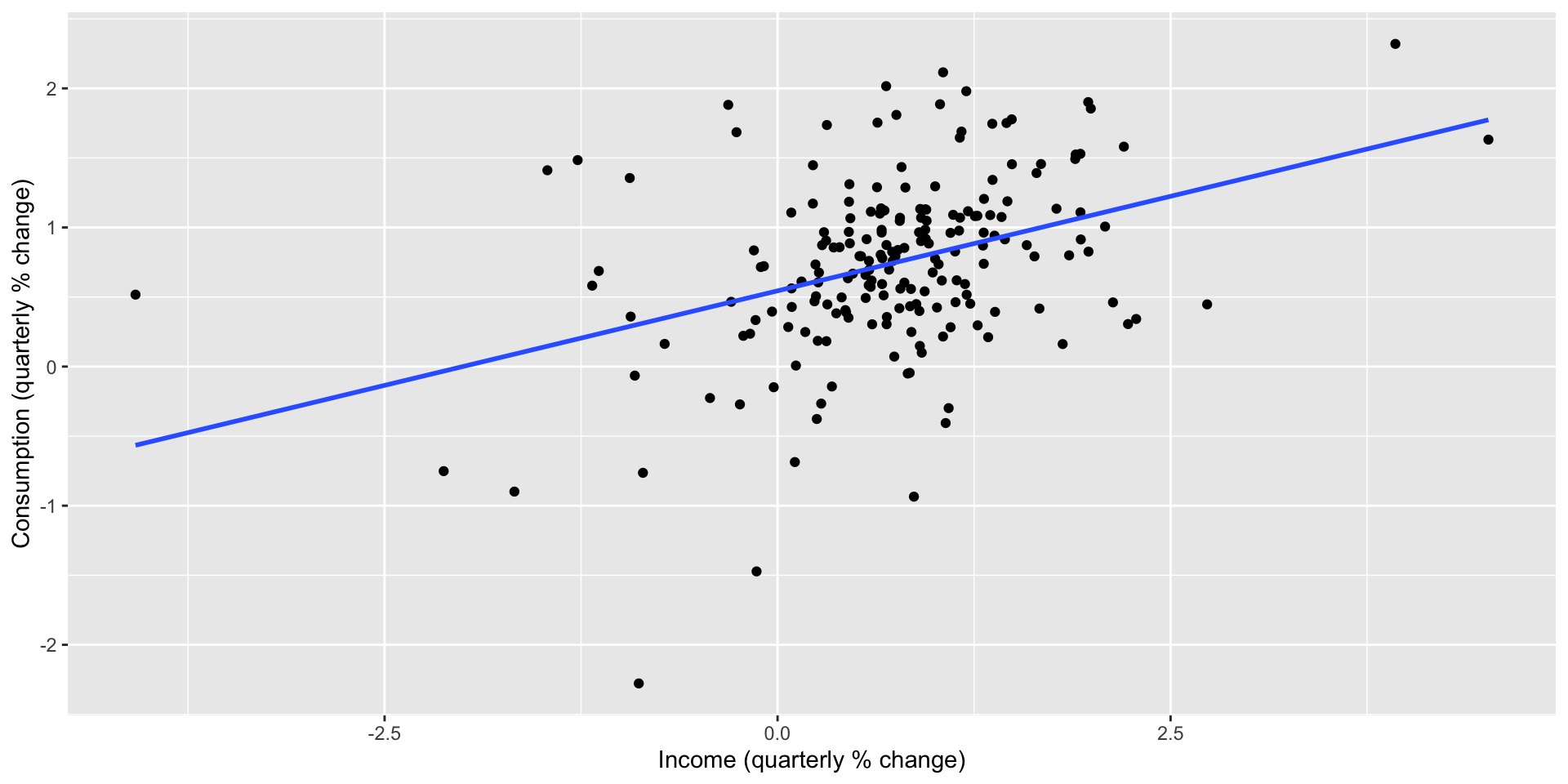
Estimating a regression function
- Suppose we want to estimate the following regression fucntion: \(y_{t} = \beta_{0} + \beta_{1} x_{t} + \epsilon_{t}\).
- Use
TSLM()to do so:
us_change |>
model(TSLM(Consumption ~ Income)) |>
report()- Use
TSLM()instead oflm()because it has time series-friendly options built in.
Regression results
Series: Consumption
Model: TSLM
Residuals:
Min 1Q Median 3Q Max
-2.58236 -0.27777 0.01862 0.32330 1.42229
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.54454 0.05403 10.079 < 2e-16 ***
Income 0.27183 0.04673 5.817 2.4e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5905 on 196 degrees of freedom
Multiple R-squared: 0.1472, Adjusted R-squared: 0.1429
F-statistic: 33.84 on 1 and 196 DF, p-value: 2.4022e-08Multiple linear regression
- Regression with more than one regressor is called multiple regression: \(y_{t} = \beta_{0} + \beta_{1} x_{1,t} + \beta_{2} x_{2,t} + ... + \beta_{k} x_{k,t} + \epsilon_{t}\)
- Coefficients reflect conditional marginal effects
Multiple regression
- Pick a few variables in
us_changeto include in a multiple regression againstConsumption.
Consumption/production
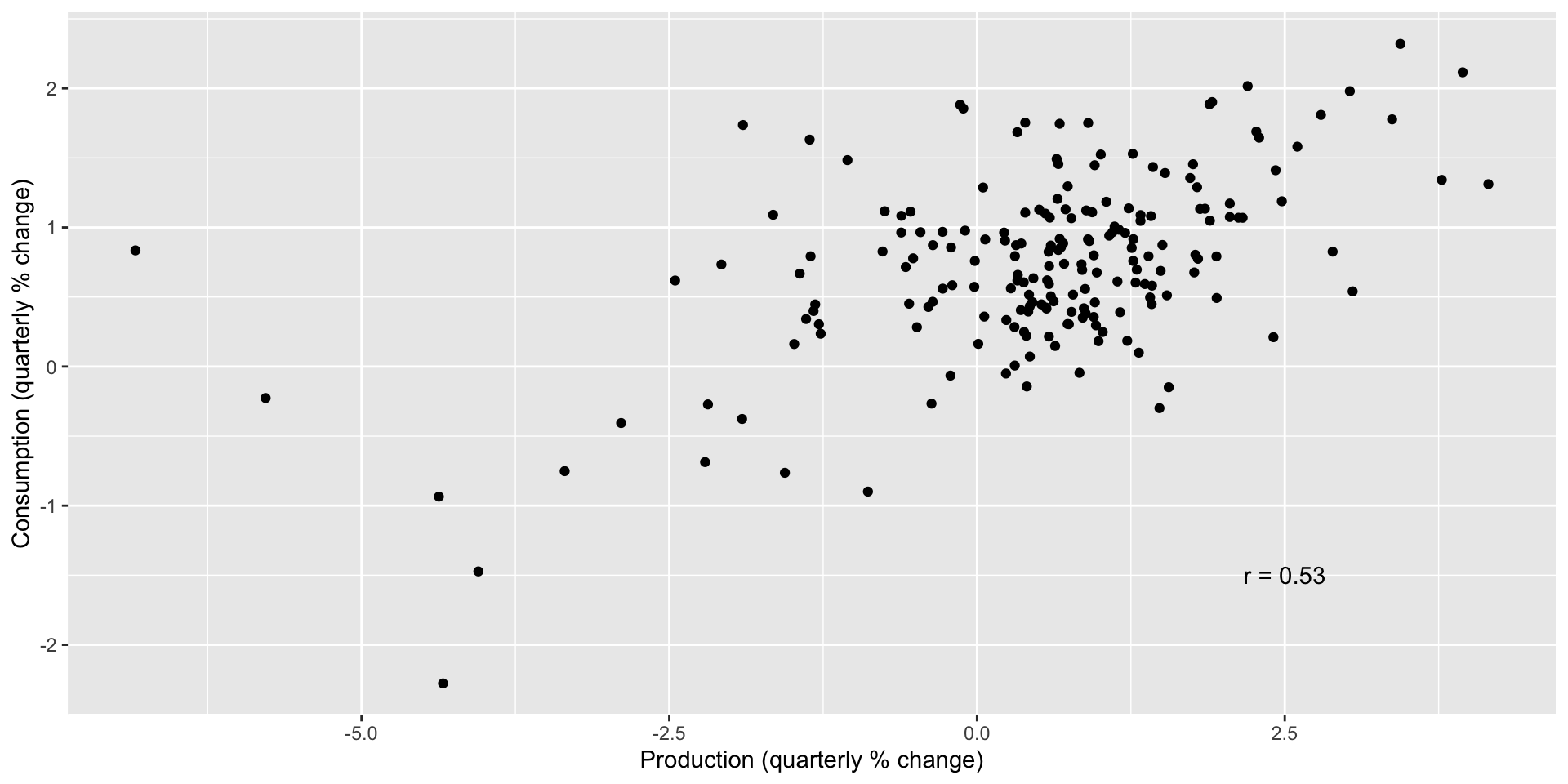
Consumption/savings
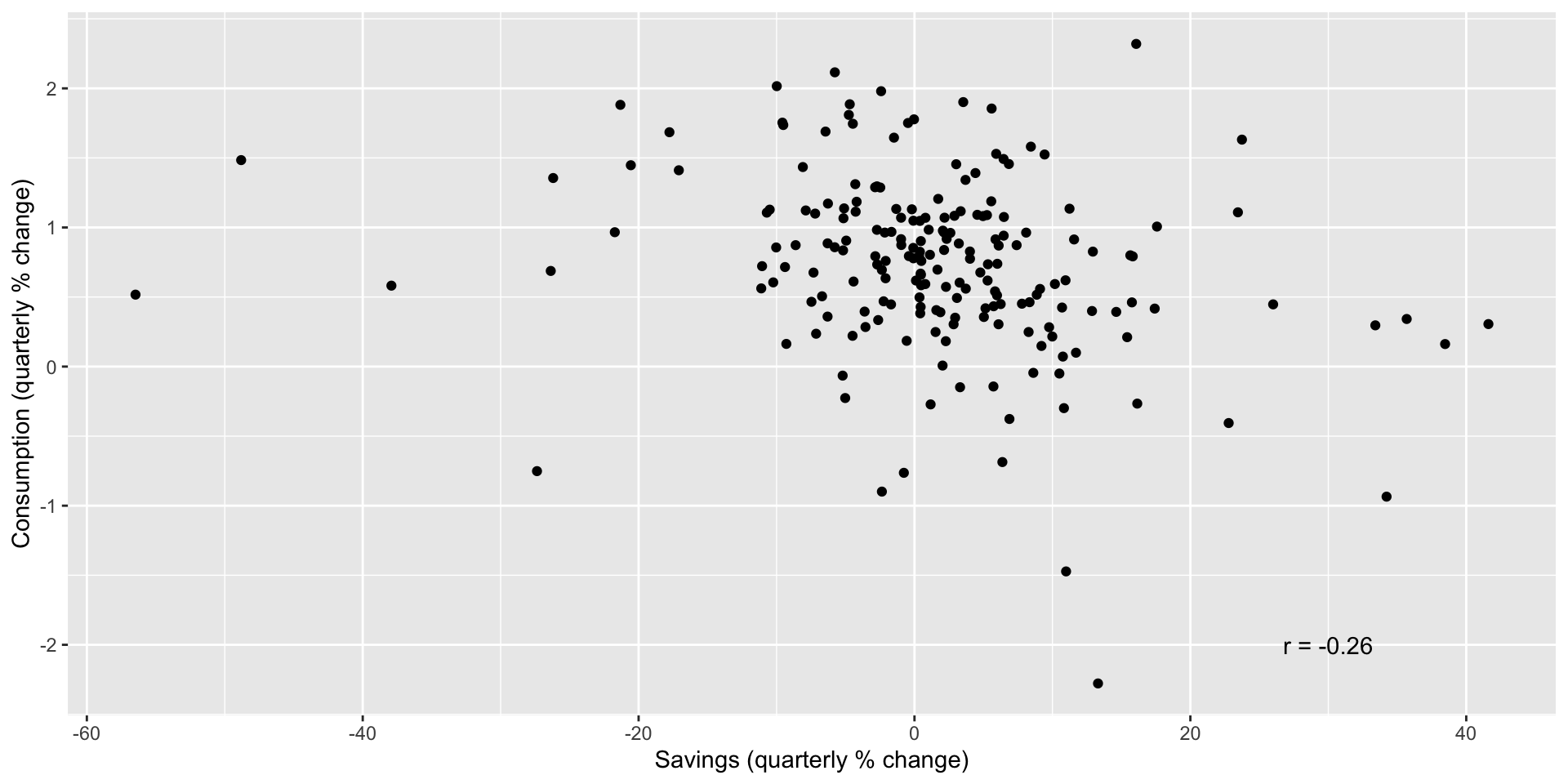
Consumption/unemployment
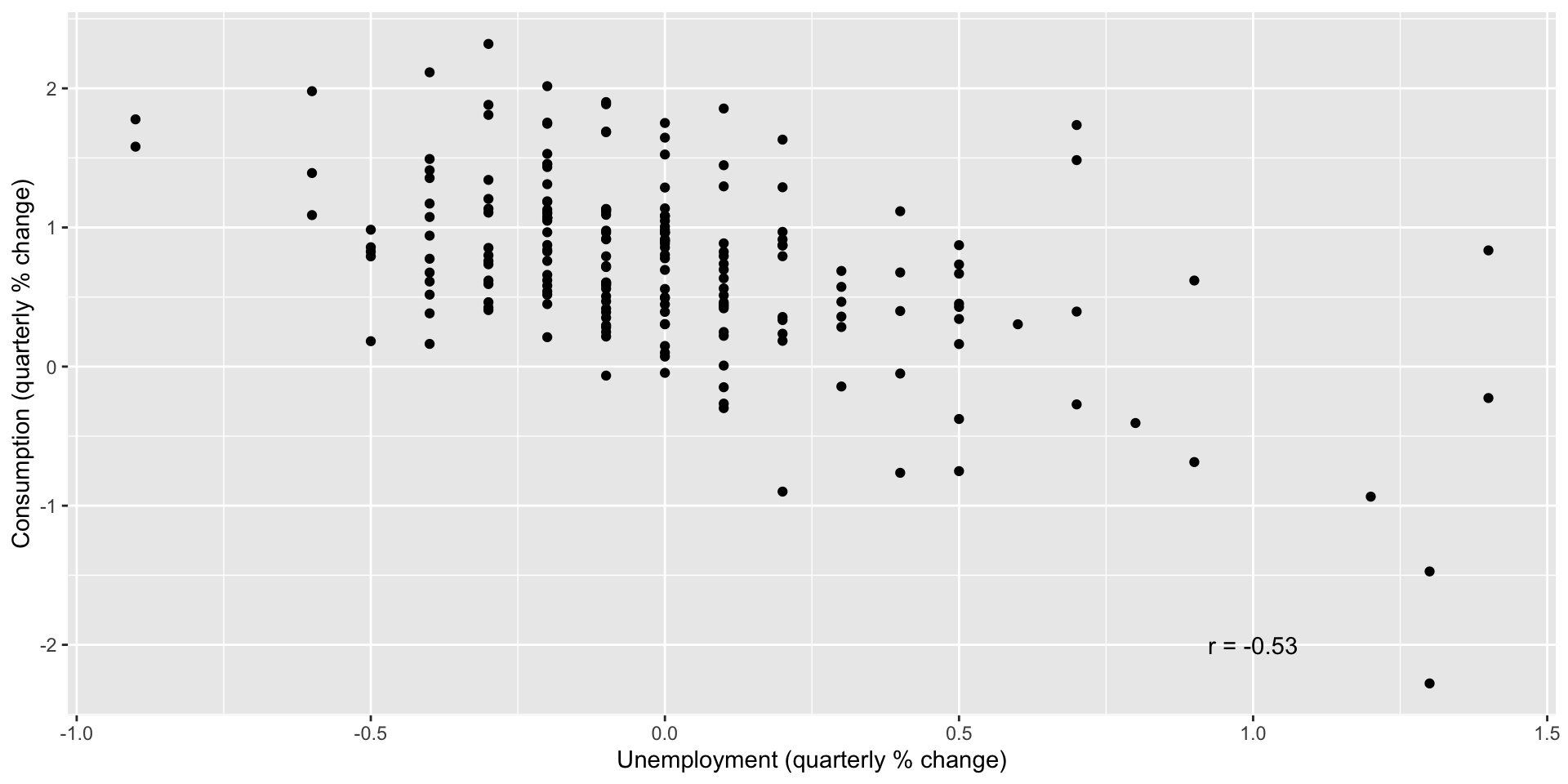
Multiple regression model
mr_c <- us_change |>
model(TSLM(Consumption ~ Income + Production + Unemployment))
report(mr_c)Multiple regression results
Series: Consumption
Model: TSLM
Residuals:
Min 1Q Median 3Q Max
-1.5973206 -0.3317848 -0.0004972 0.2948522 1.6881414
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.55973 0.04915 11.389 < 2e-16 ***
Income 0.18044 0.04175 4.322 2.47e-05 ***
Production 0.10227 0.03756 2.722 0.00707 **
Unemployment -0.49026 0.15376 -3.188 0.00167 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.508 on 194 degrees of freedom
Multiple R-squared: 0.3755, Adjusted R-squared: 0.3658
F-statistic: 38.88 on 3 and 194 DF, p-value: < 2.22e-16Fitted values
- Estimating the regression allows us to obtain fitted (predicted) values for \(y\): \(\hat{y}_{t} = \hat{\beta}_{0} + \hat{\beta}_{1} x_{1,t} + \hat{\beta}_{2} x_{2,t} + ... + \hat{\beta}_{k} x_{k,t} + \epsilon_{t}\)
- Note these are predictions for the actual observed values, not forecasts.
Accessing fitted values
- With a
tslmobject, useaugment()to access fitted values:
augment(mr_c)# A tsibble: 198 x 6 [1Q]
# Key: .model [1]
.model Quarter Consumption .fitted .resid .innov
<chr> <qtr> <dbl> <dbl> <dbl> <dbl>
1 TSLM(Consumption ~ Income + Prod… 1970 Q1 0.619 0.0562 0.562 0.562
2 TSLM(Consumption ~ Income + Prod… 1970 Q2 0.452 0.479 -0.0274 -0.0274
3 TSLM(Consumption ~ Income + Prod… 1970 Q3 0.873 0.564 0.309 0.309
4 TSLM(Consumption ~ Income + Prod… 1970 Q4 -0.272 -0.0502 -0.222 -0.222
5 TSLM(Consumption ~ Income + Prod… 1971 Q1 1.90 1.16 0.741 0.741
6 TSLM(Consumption ~ Income + Prod… 1971 Q2 0.915 0.962 -0.0470 -0.0470
7 TSLM(Consumption ~ Income + Prod… 1971 Q3 0.794 0.636 0.158 0.158
8 TSLM(Consumption ~ Income + Prod… 1971 Q4 1.65 1.00 0.642 0.642
9 TSLM(Consumption ~ Income + Prod… 1972 Q1 1.31 1.17 0.146 0.146
10 TSLM(Consumption ~ Income + Prod… 1972 Q2 1.89 0.988 0.897 0.897
# ℹ 188 more rowsPlotting fitted values
- Let’s see how well our predicted values line up with reality.
augment(mr_c) |>
ggplot(aes(x = Quarter)) +
geom_line(aes(y = Consumption, colour = "Data")) +
geom_line(aes(y = .fitted, colour = "Fitted")) +
labs(y = NULL,
title = "Percent change in consumption expenditure") +
scale_colour_manual(values=c(Data="black",Fitted="red")) +
guides(colour = guide_legend(title = NULL))Plotting fitted values
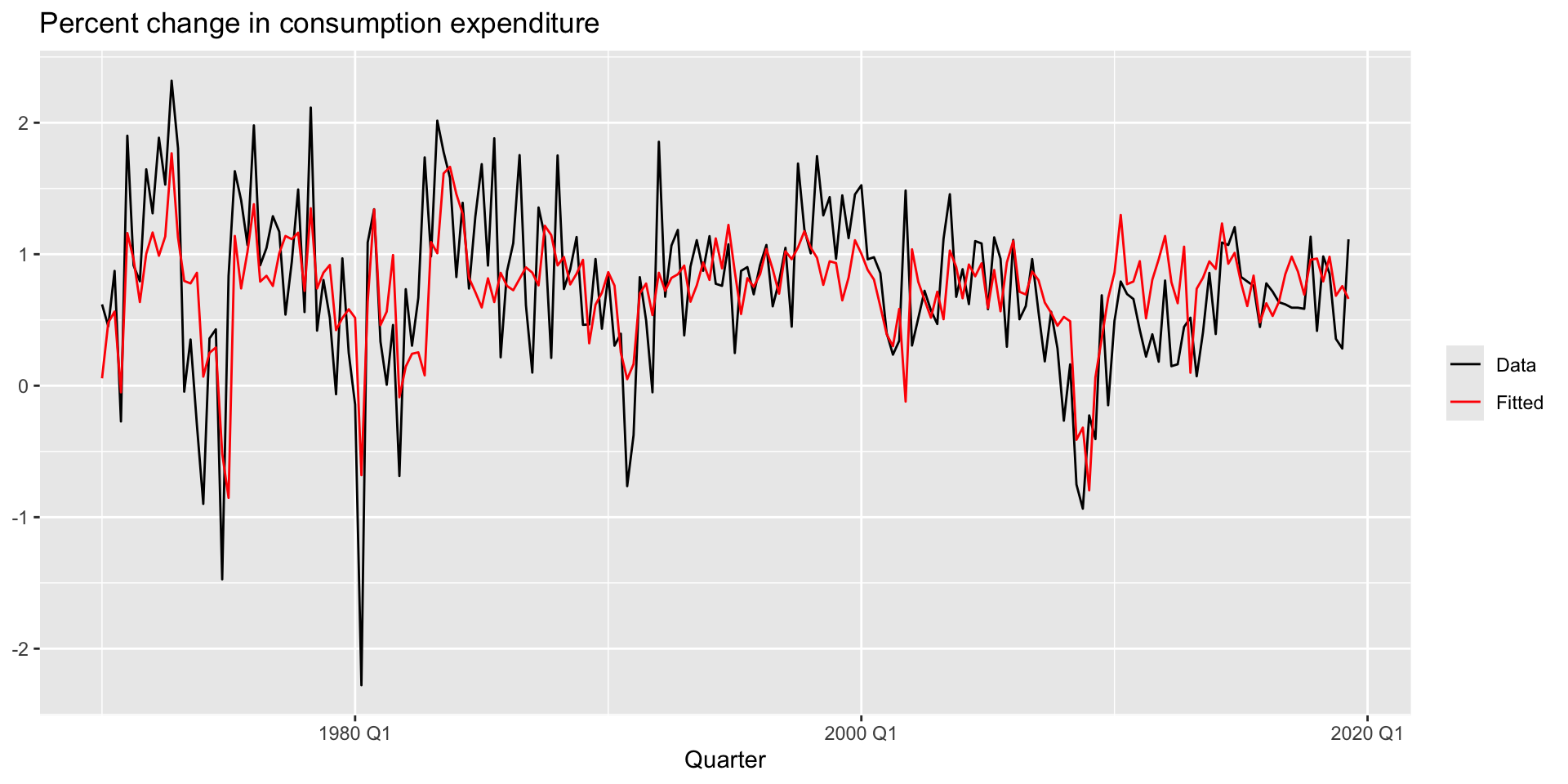
Plotting fitted values: scatter
- We could scatter \(y\) against \(\hat{y}\):
augment(mr_c) |>
ggplot(aes(x = Consumption, y = .fitted)) +
geom_point() +
labs(x = "Data",
y = "Fitted values",
title = "% change in consumption expenditure") +
geom_abline(intercept = 0, slope = 1)Plotting fitted values: scatter
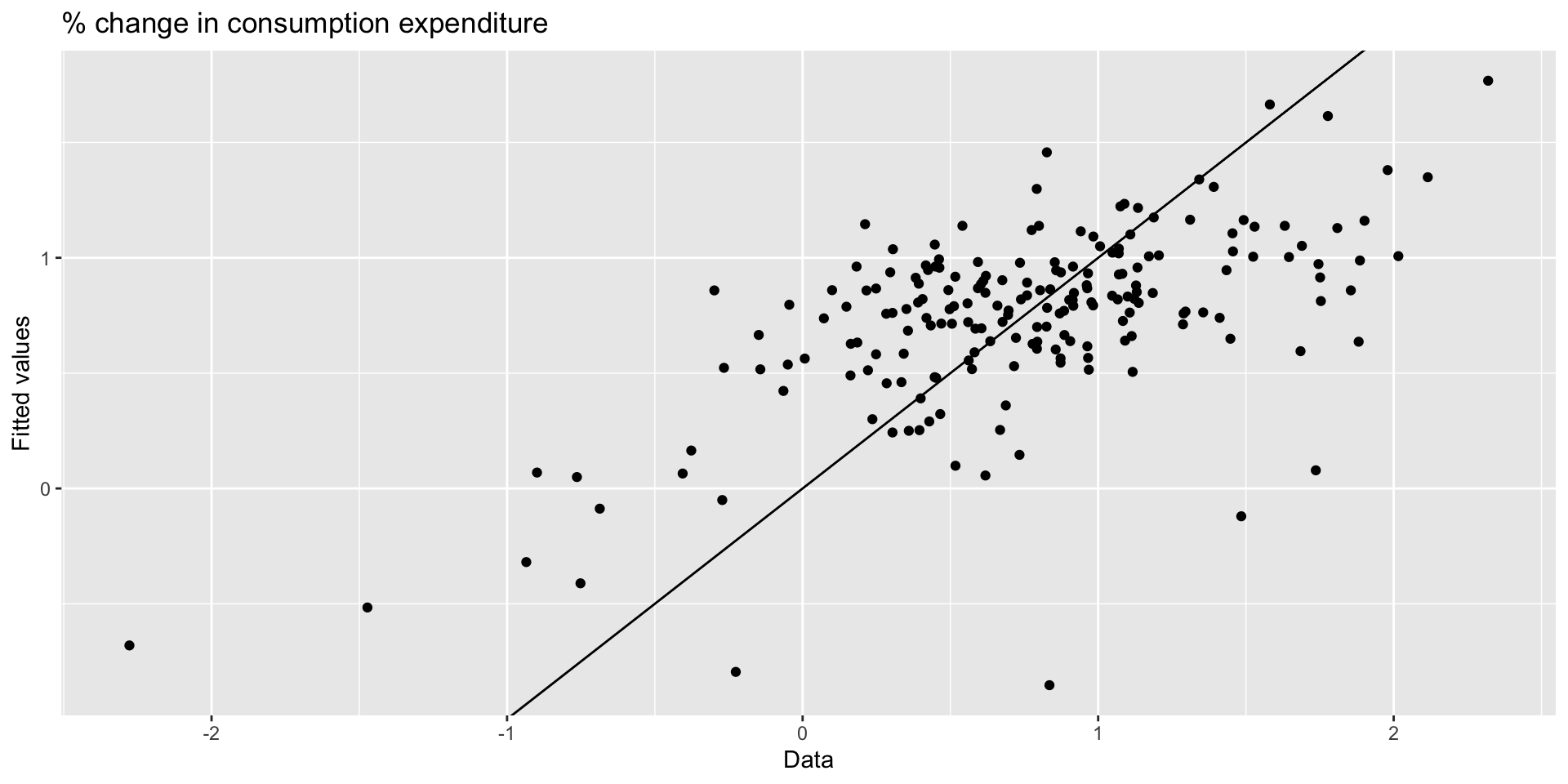
Goodness-of-fit
- The coefficient of determination, \(R^{2}\) is a good summary measure of how well your model fits the data:
\(R^{2} = \frac{\sum(\hat{y}_{t} - \bar{y})^{2}}{\sum(y_{t} - \bar{y})^{2}}\)
- It gives the proportion of variation in \(y\) explained by \(\hat{y}\).
- Note \(R^{2}\) never decreases when adding predictors. Not necessarily a good metric for evaluating a forecast model.
- \(R^{2}\) of above model is 0.3755.