More time series graphics

BUS 323 Forecasting and Risk Analysis

Seasonal plots

Seasonal plots disaggregate a time series into “seasons”.
I’m going to work with the antidiabetic drug sales object we made last time to start:

library(fpp3)
a10 <- PBS |>
  filter(ATC2 == "A10") |>
  select(Month, Concession, Type, Cost) |>
  summarise(TotalC = sum(Cost)) |>
  mutate(Cost = TotalC/1e6)

Seasonal plots

To make a seasonal plot, use gg_season()
e.g.

a10 |>
  gg_season(Cost, labels="right") +
  labs(y = "$ (millions)",
    title = "Antidiabetic drug sales by year")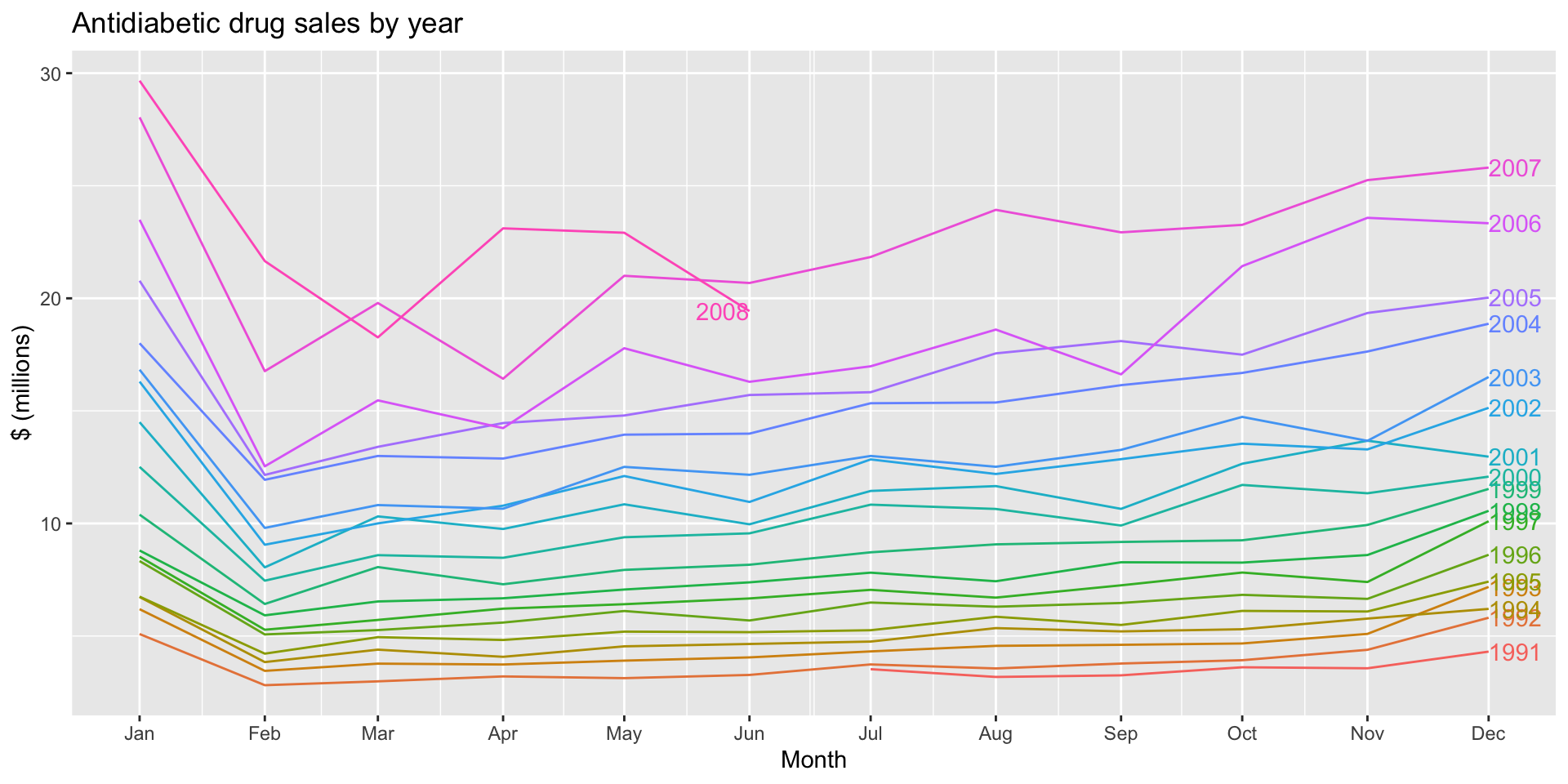

Seasonal plots

?gg_season()
gg_season will assume you want to disaggregate by the largest frequency in the tsibble by default.

Seasonal plots

If your time series has multiple periods, you can specify which seasonal plot you want using the period argument.
vic_elec has half-hourly observations of electricity demand in Victoria. What does gg_season plot by default?

vic_elec |>
  gg_season(Demand) +
  labs(y="MWh", title="Electricity demand, Victoria")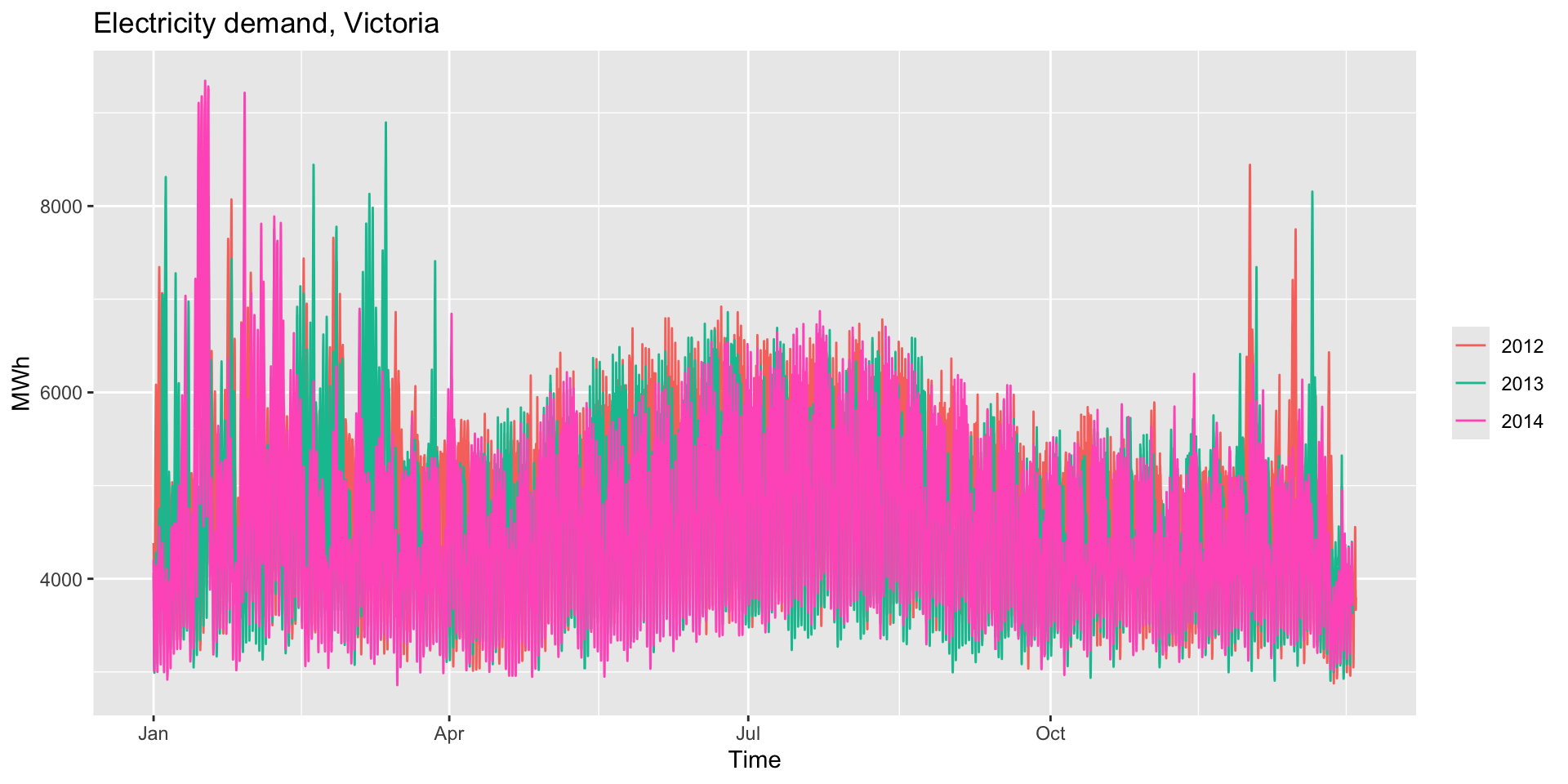

Seasonal plots

Try head(vic_elec) to get a sense of the format of the time variable.
Use the period argument to produce a daily seasonal time plot:

vic_elec |>
  gg_season(Demand, period="day") +
  labs(y="MWh", title="Electricity demand by day, Victoria")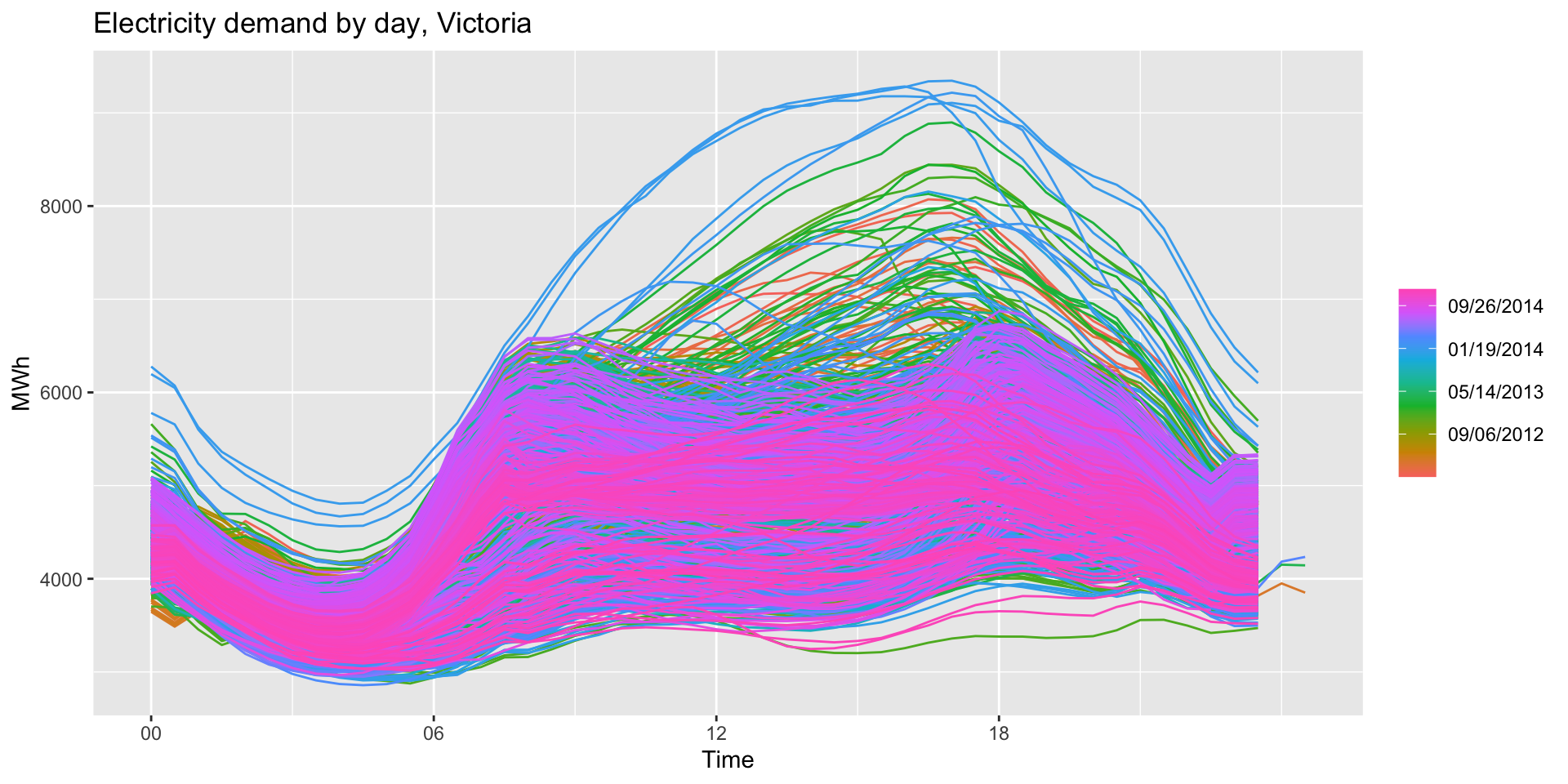

Seasonal plots

A weekly time plot:

vic_elec |>
  gg_season(Demand, period="week") +
  labs(y="MWh", title="Electricity demand by week, Victoria")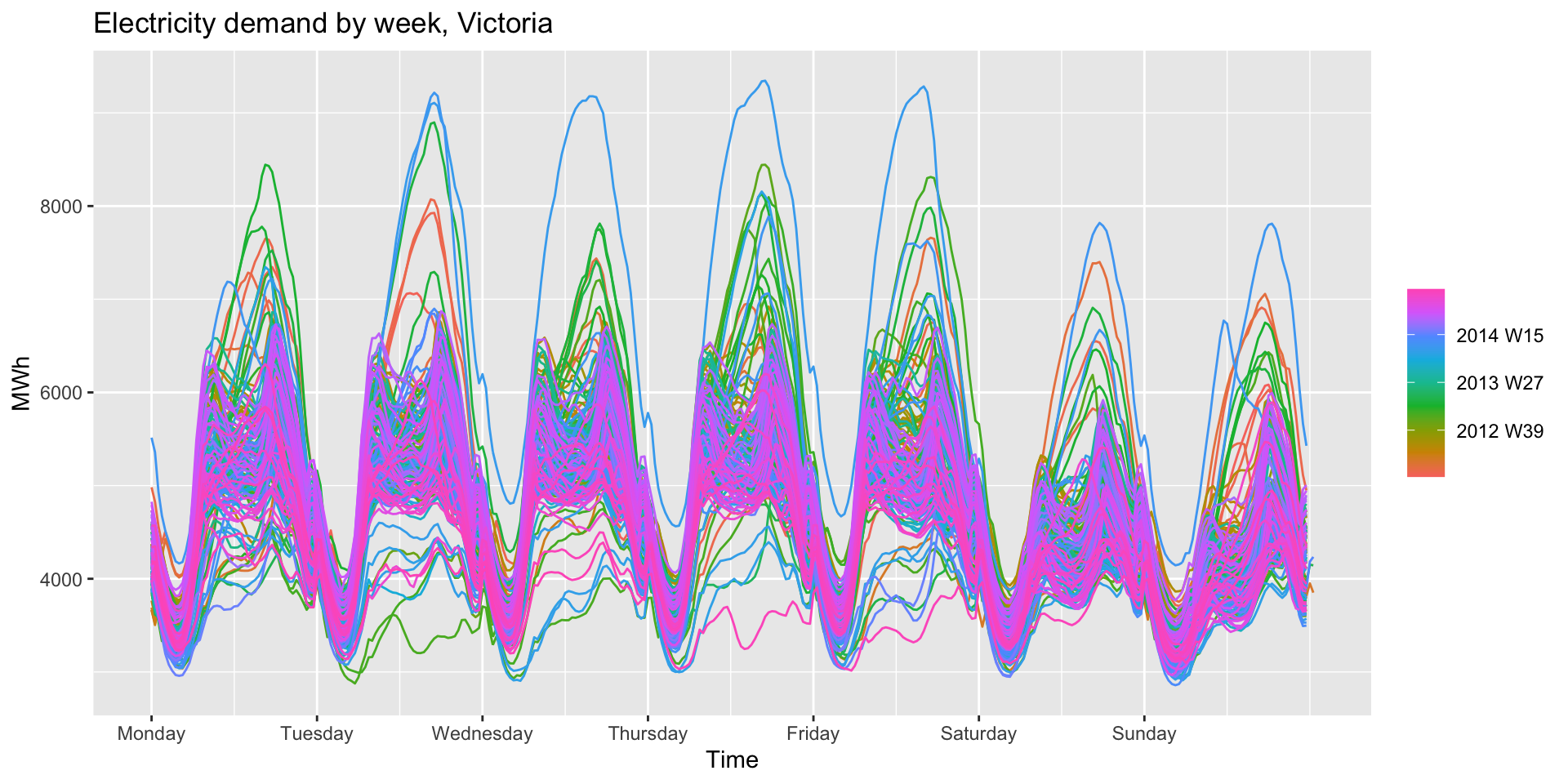

Seasonal subseries plots

gg_subseries()
Plots a time series by each season within a seasonal period.
e.g., using the antidiabetic drug sales dataset:

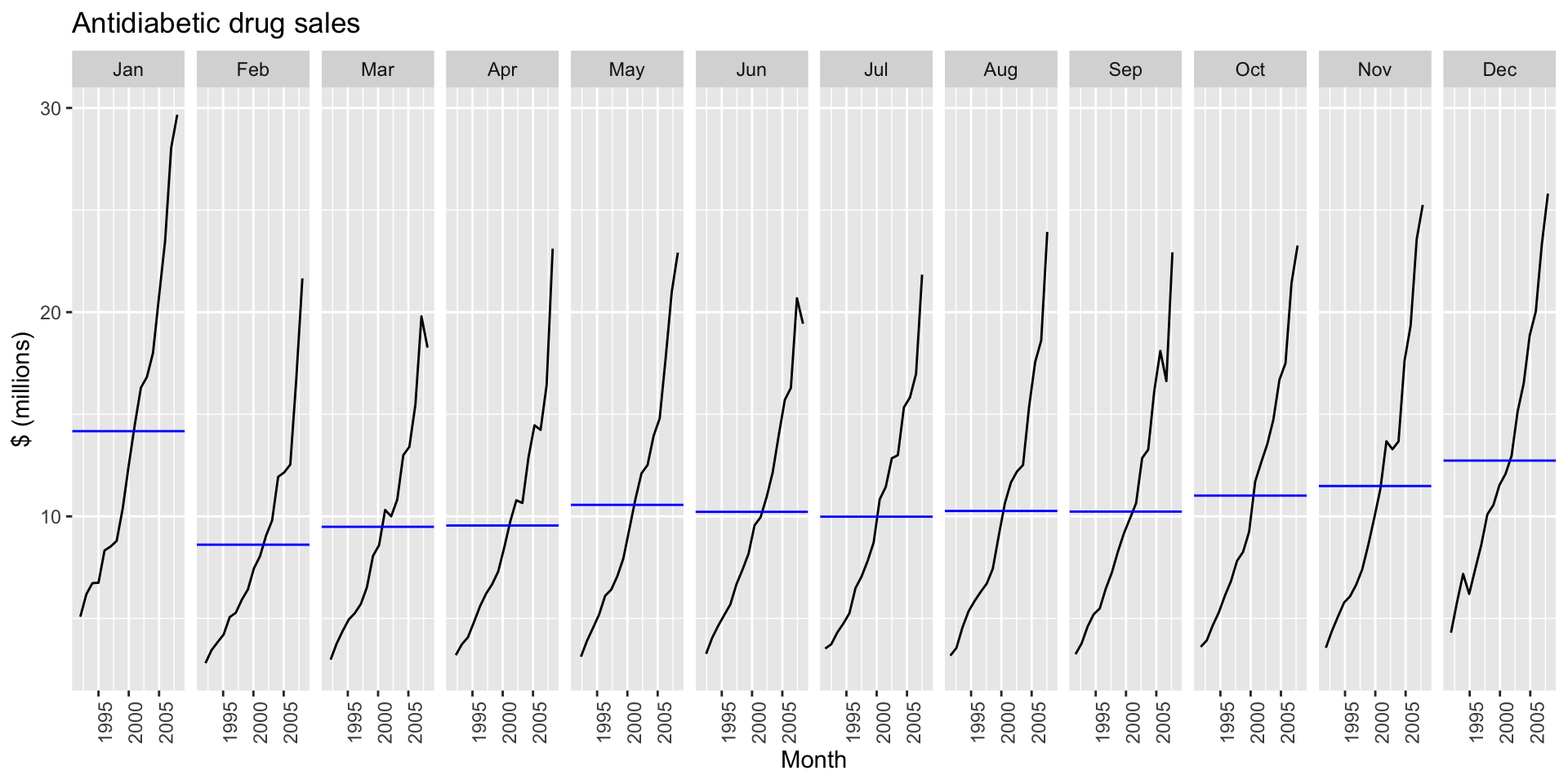
a10 |>
  gg_subseries(Cost) +
  labs(
    y = "$ (millions)",
    title = "Antidiabetic drug sales"
  )

Seasonal subseries plots

Exercise: holiday tourism

holidays <- tourism |>
  filter(Purpose == "Holiday") |>
  group_by(State) |>
  summarise(Trips = sum(Trips))

# A tsibble: 640 x 3 [1Q]
# Key:       State [8]
   State Quarter Trips
   <chr>   <qtr> <dbl>
 1 ACT   1998 Q1  196.
 2 ACT   1998 Q2  127.
 3 ACT   1998 Q3  111.
 4 ACT   1998 Q4  170.
 5 ACT   1999 Q1  108.
 6 ACT   1999 Q2  125.
 7 ACT   1999 Q3  178.
 8 ACT   1999 Q4  218.
 9 ACT   2000 Q1  158.
10 ACT   2000 Q2  155.
# ℹ 630 more rows

Exercise: holiday tourism autoplot

autoplot(holidays, Trips) +
  labs(y = "Overnight trips (thousands)",
  title = "Holiday trips by state")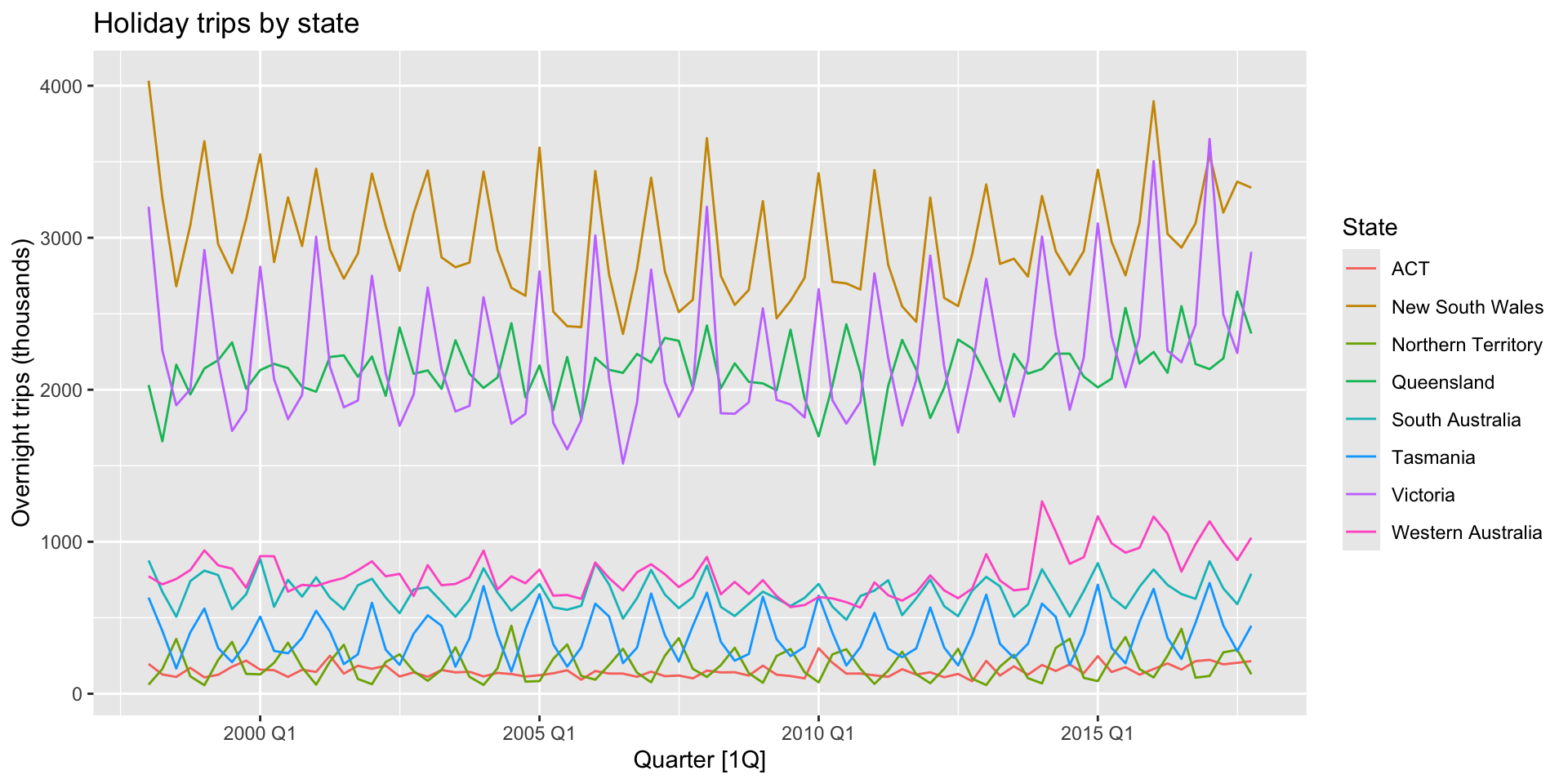

Exercise: holiday tourism seasonal plot

gg_season(holidays, Trips) +
  labs(y = "Overnight trips (thousands)",
  title = "Holiday trips by state and year")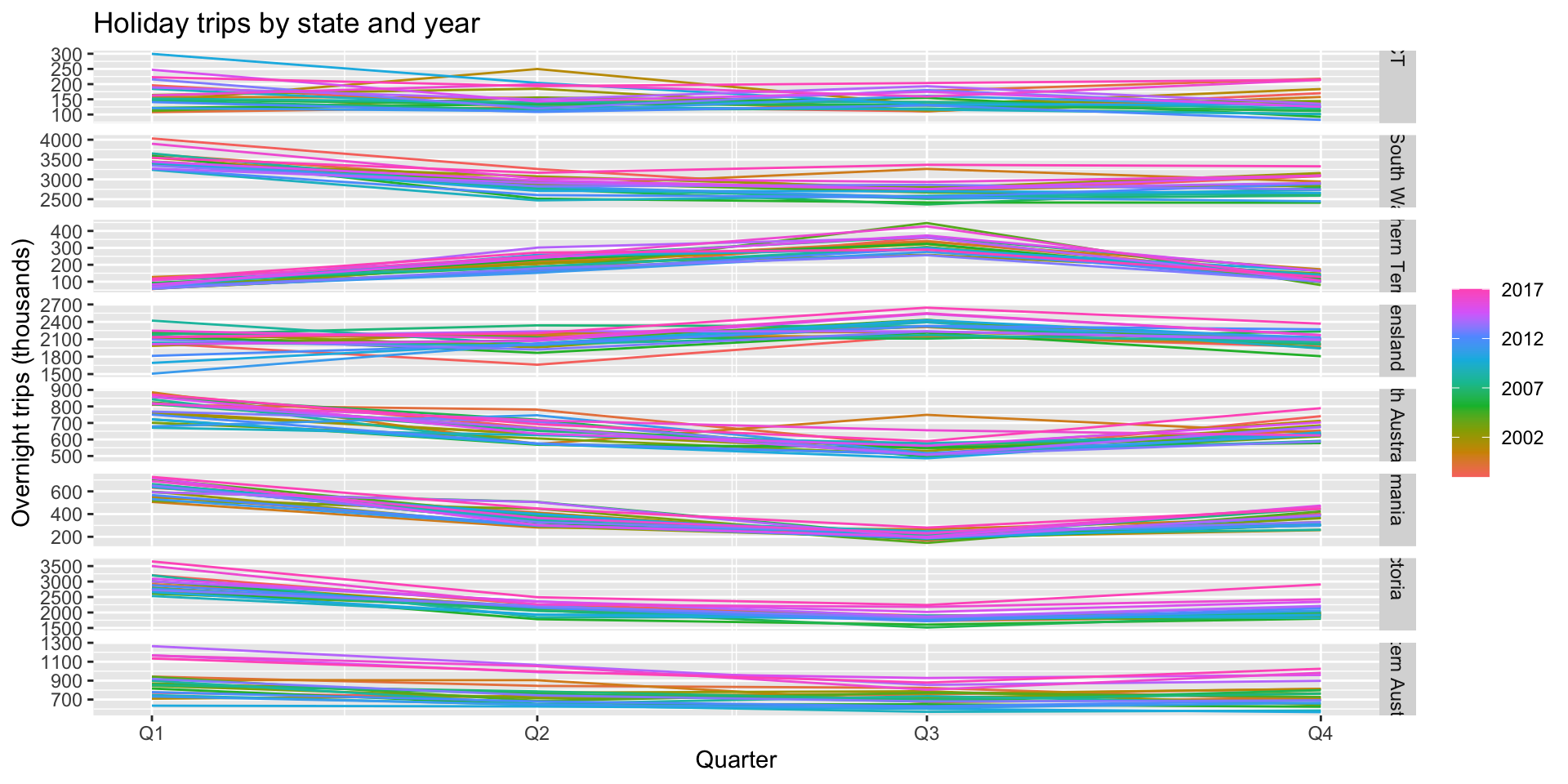

Exercise: holiday tourism subseries plots

gg_subseries(holidays, Trips) +
  labs(y = "Overnight trips (thousands)",
  title = "Holiday trips by state and quarter")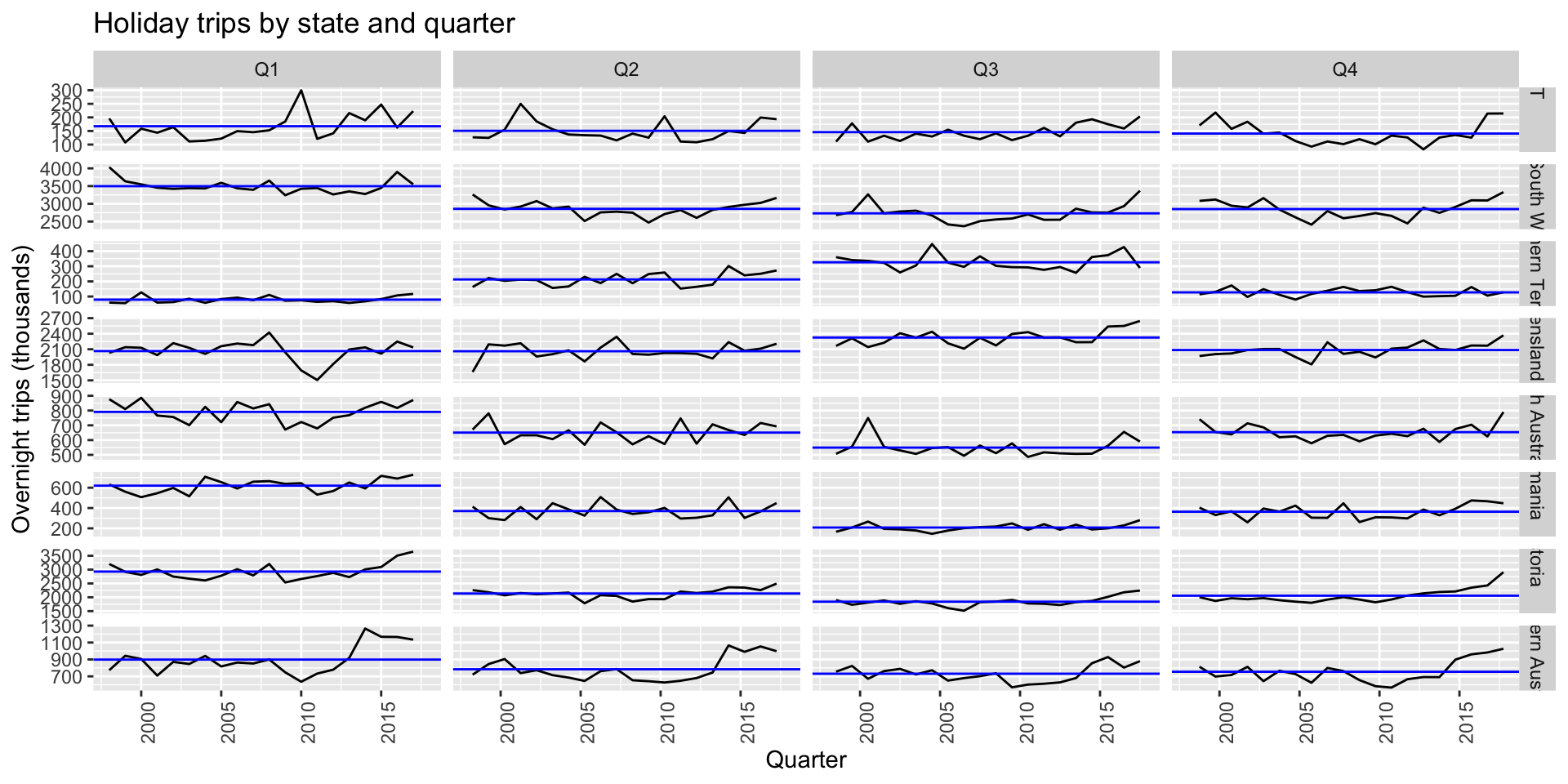

Scatterplots

Useful for visualizing relationships between variables.

Scatterplots

Suppose we think electricity demand and temperature are related. Here’s demand:

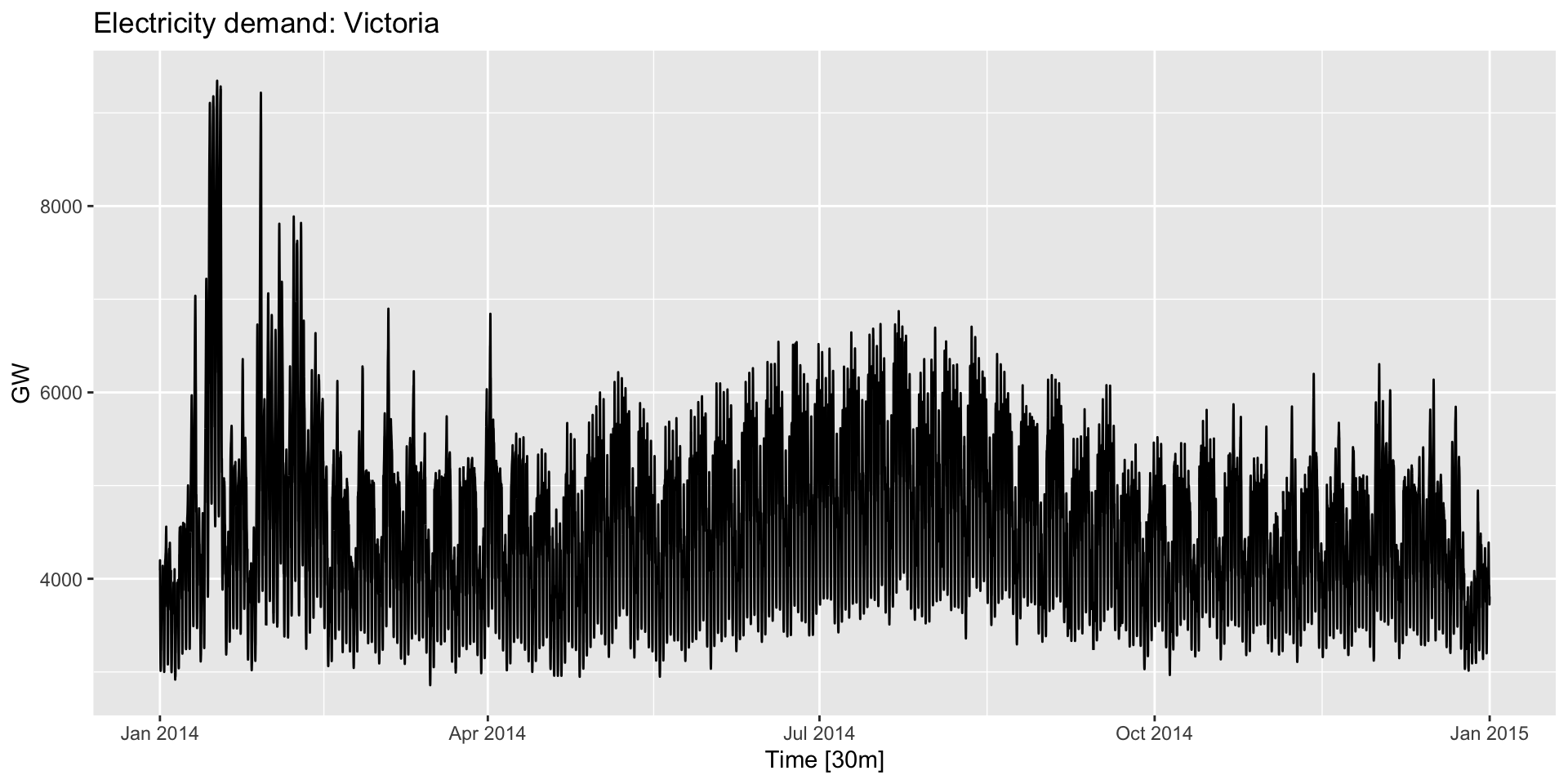
Scatterplots

Here’s temperature:

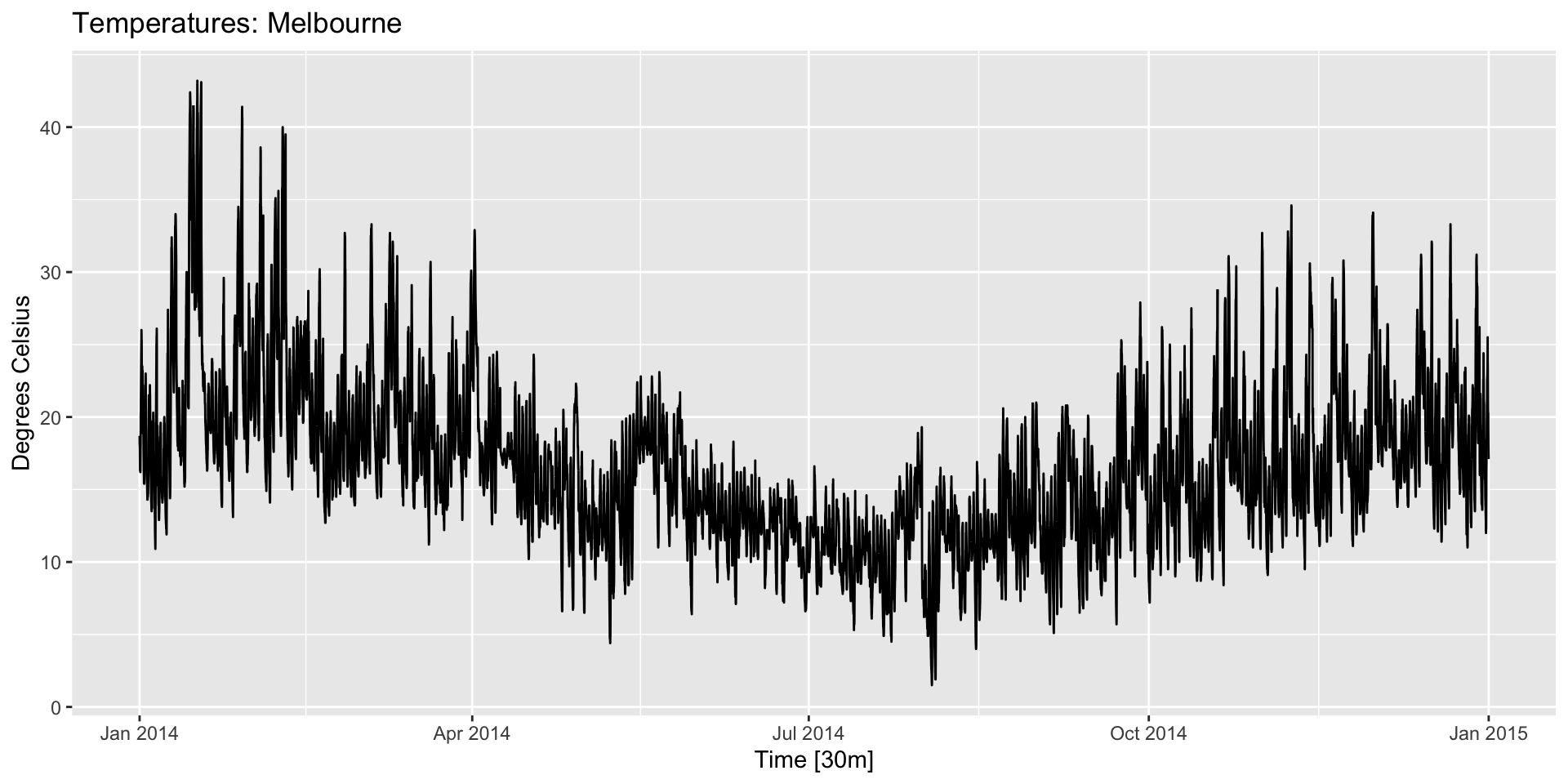
Scaterplots

Here’s a scatterplot:

vic_elec |>
  filter(year(Time) == 2014) |>
  ggplot(aes(x = Temperature, y = Demand)) +
  geom_point() +
  labs(title="Electricity demand and temperature",
       x = "Temperature (Celsius)",
       y = "Electricity demand (GW)")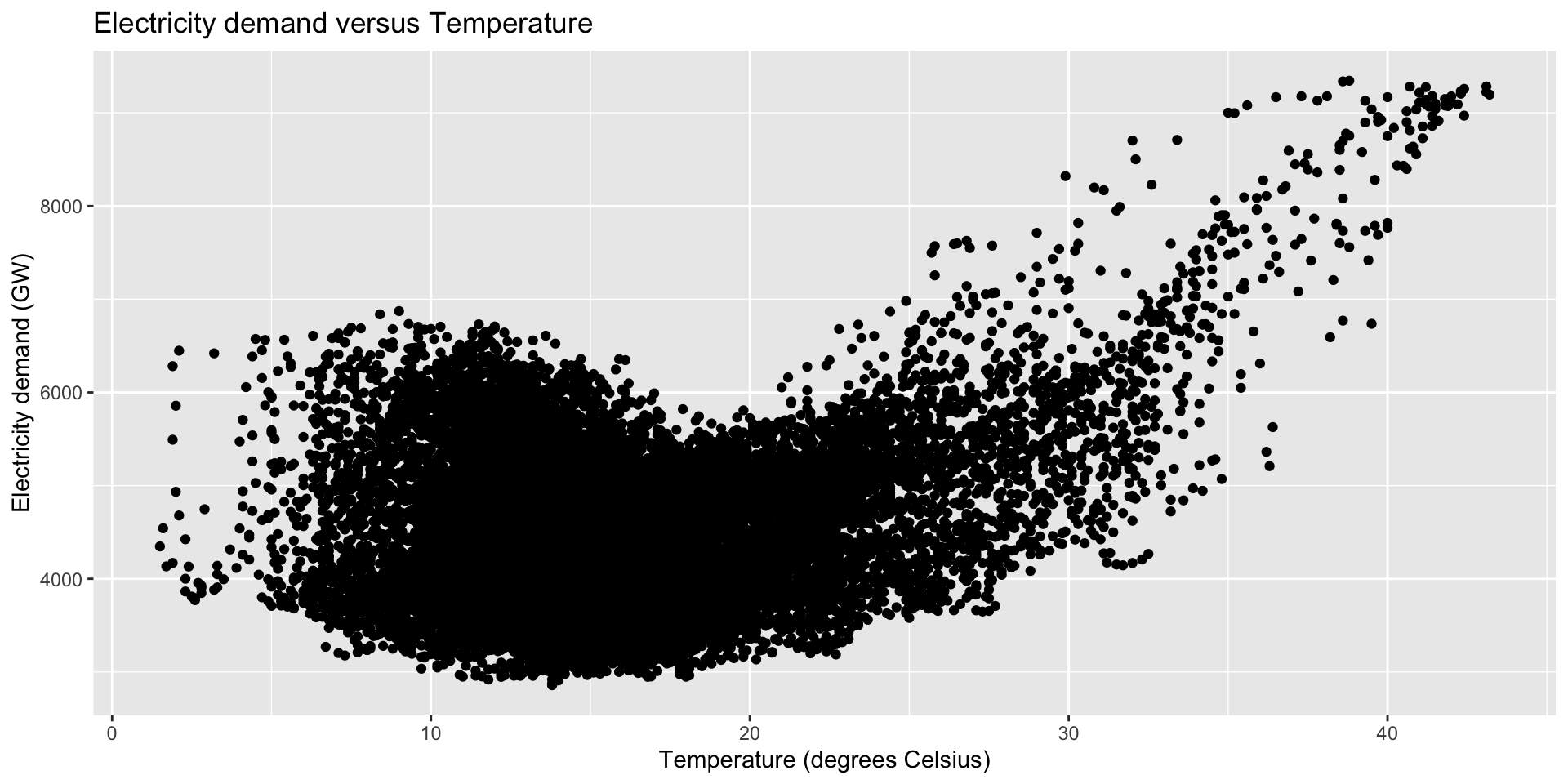

Lag plots

Lagged values (\(y_{t-k}\)) are often useful predictors in forecasting.
We can use gg_lag() to get a quick sense of which might be important.

holidays |>
  filter(State == "ACT") |>
    gg_lag(Trips, geom = "point") +
    labs(x = "lag(Trips, k)")

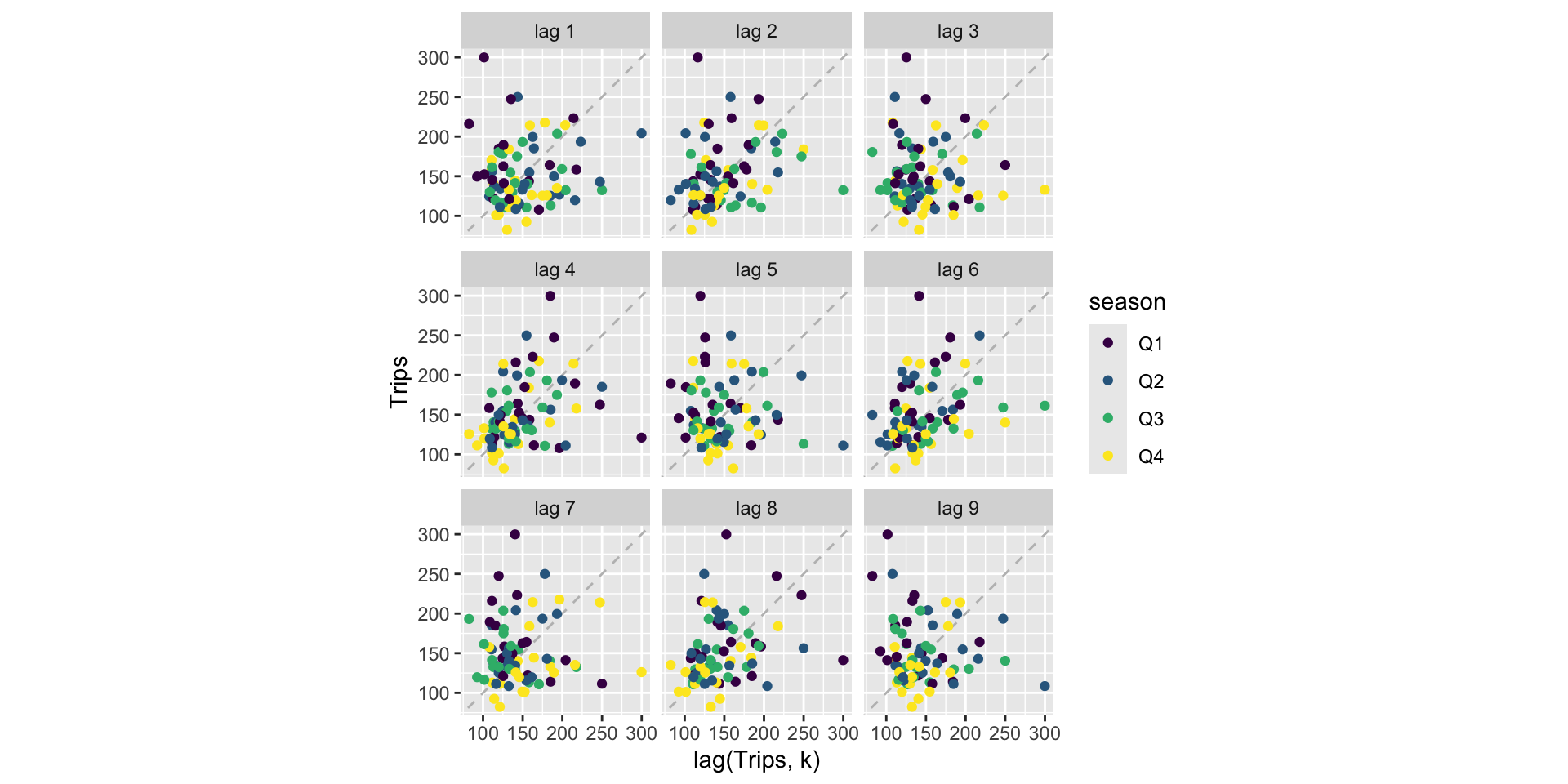
Lag plots

Not much there. Let’s try another series:

recent_production <- aus_production |>
  filter(year(Quarter) >= 2000)
autoplot(recent_production, Beer)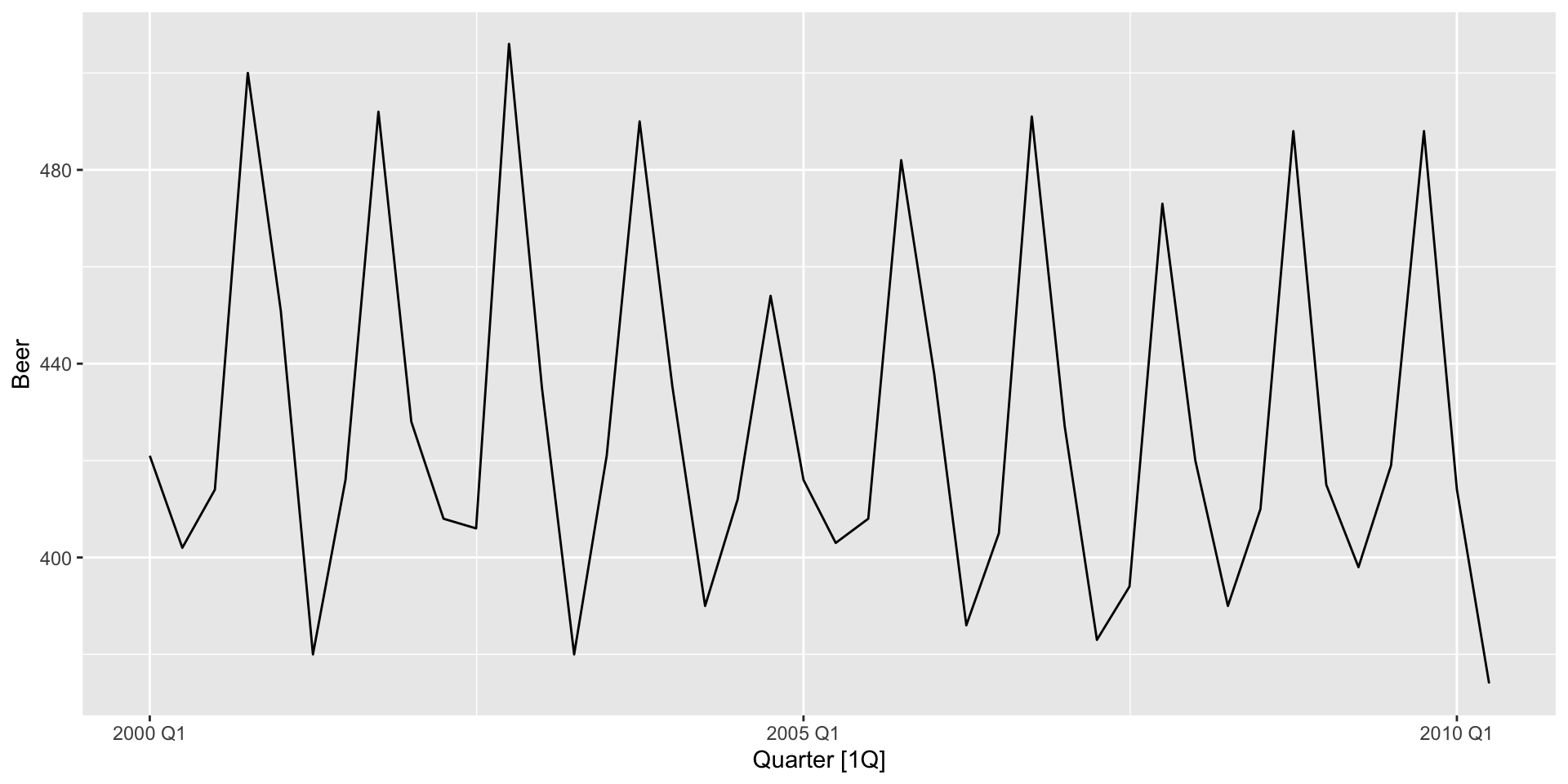

Lag plots

There’s clear seasonality across years here. Let’s see what the lag plots say:

recent_production |>
  gg_lag(Beer, geom = "point") +
  labs(x = "lag(Beer, k)")

Lag plots

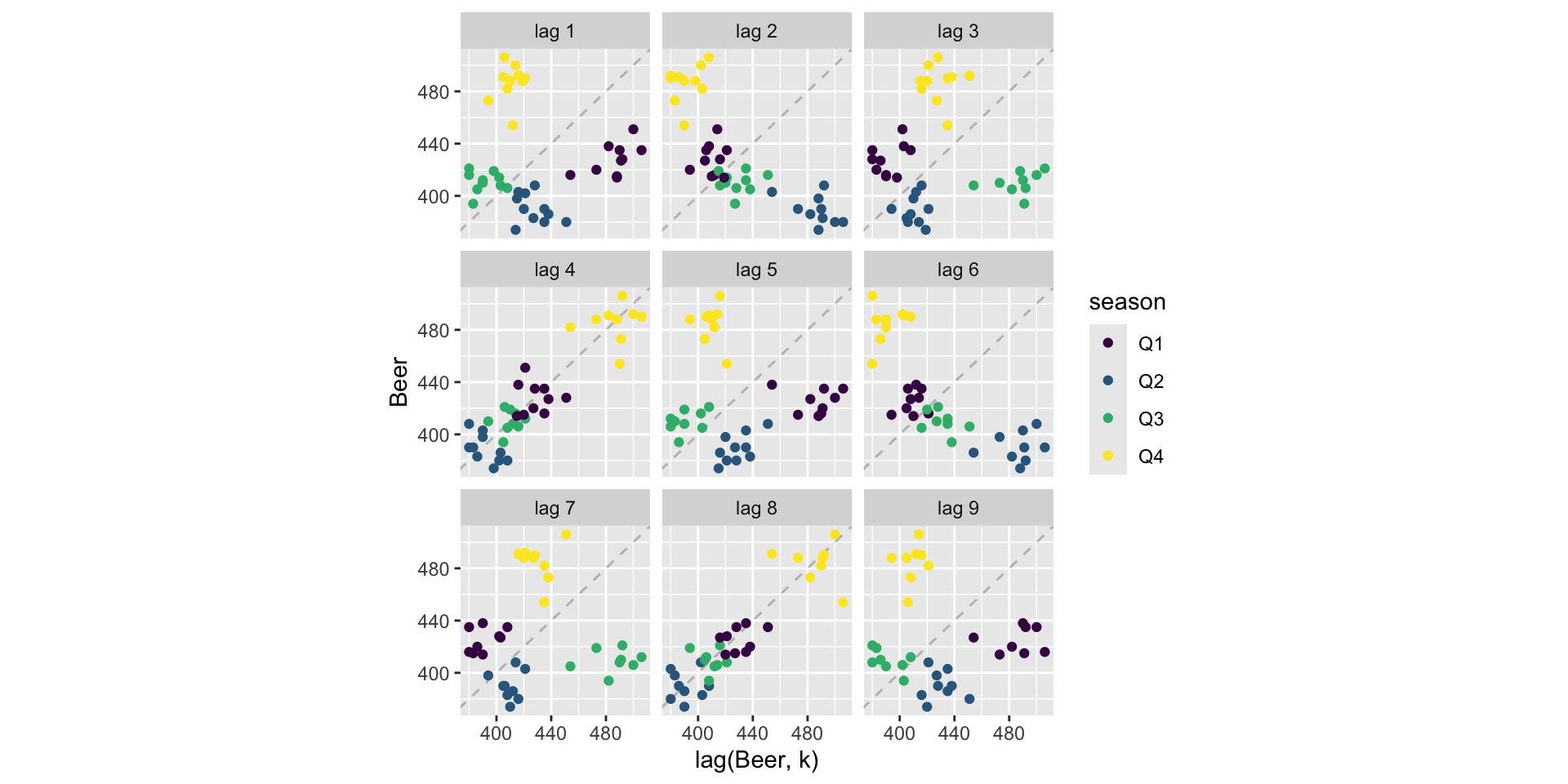
Autocorrelation and the ACF

ACF() calculates \(r_{k}\) for all \(k\) as specified by the lag_max option:

recent_production |>
  ACF(Beer, lag_max = 9)

# A tsibble: 9 x 2 [1Q]
       lag      acf
  <cf_lag>    <dbl>
1       1Q -0.0530 
2       2Q -0.758  
3       3Q -0.0262 
4       4Q  0.802  
5       5Q -0.0775 
6       6Q -0.657  
7       7Q  0.00119
8       8Q  0.707  
9       9Q -0.0888

ACF plots

We can plot the autocorrelation coefficients easily with autoplot():

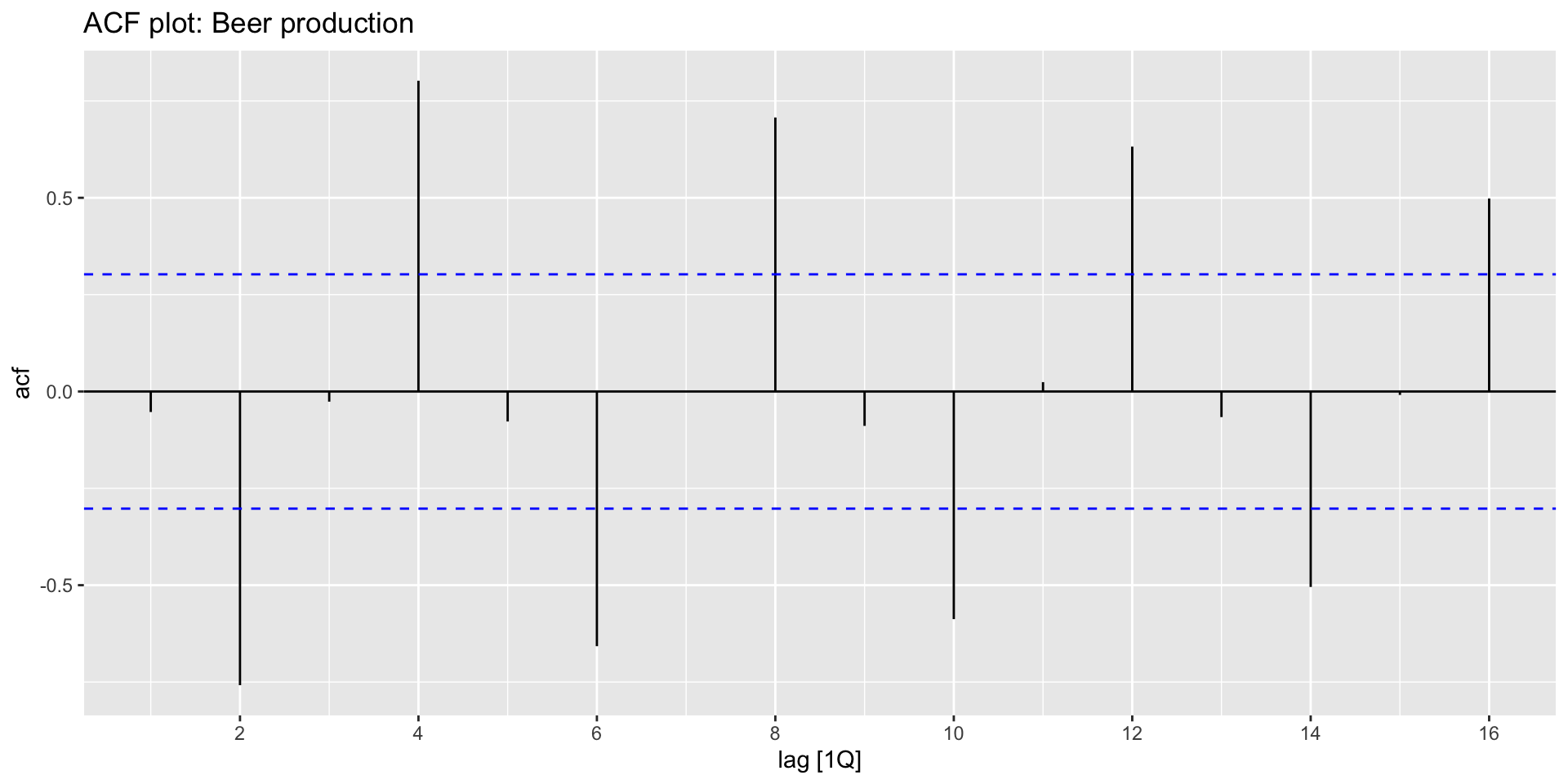
recent_production |>
  ACF(Beer) |>
    autoplot() +
    labs(title = "ACF plot: Beer production")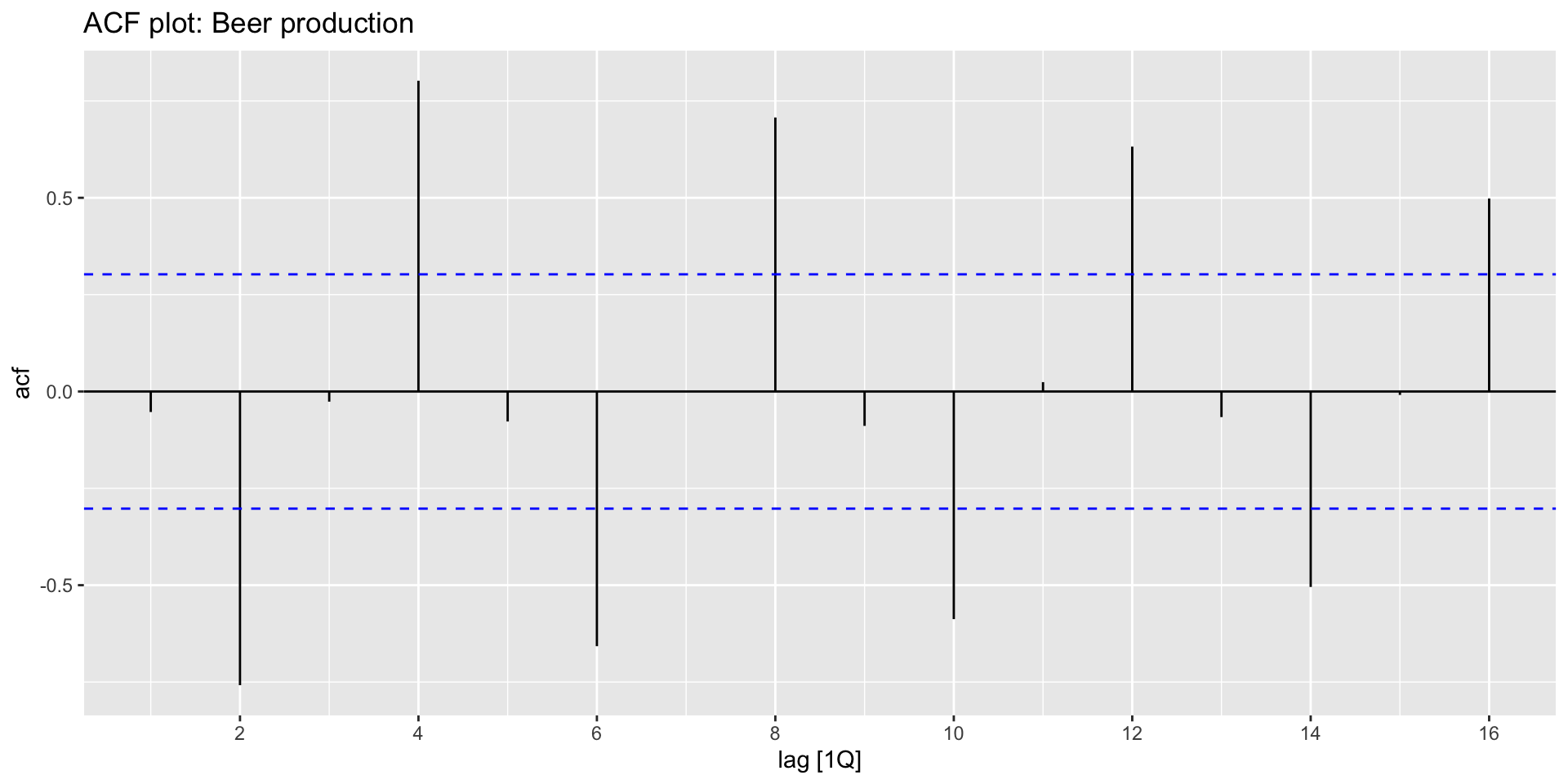

ACF plots in the presence of trend

When there is a trend, small lags tend to have high \(r_{k}\) and large lags tend to have small \(r_{k}\):

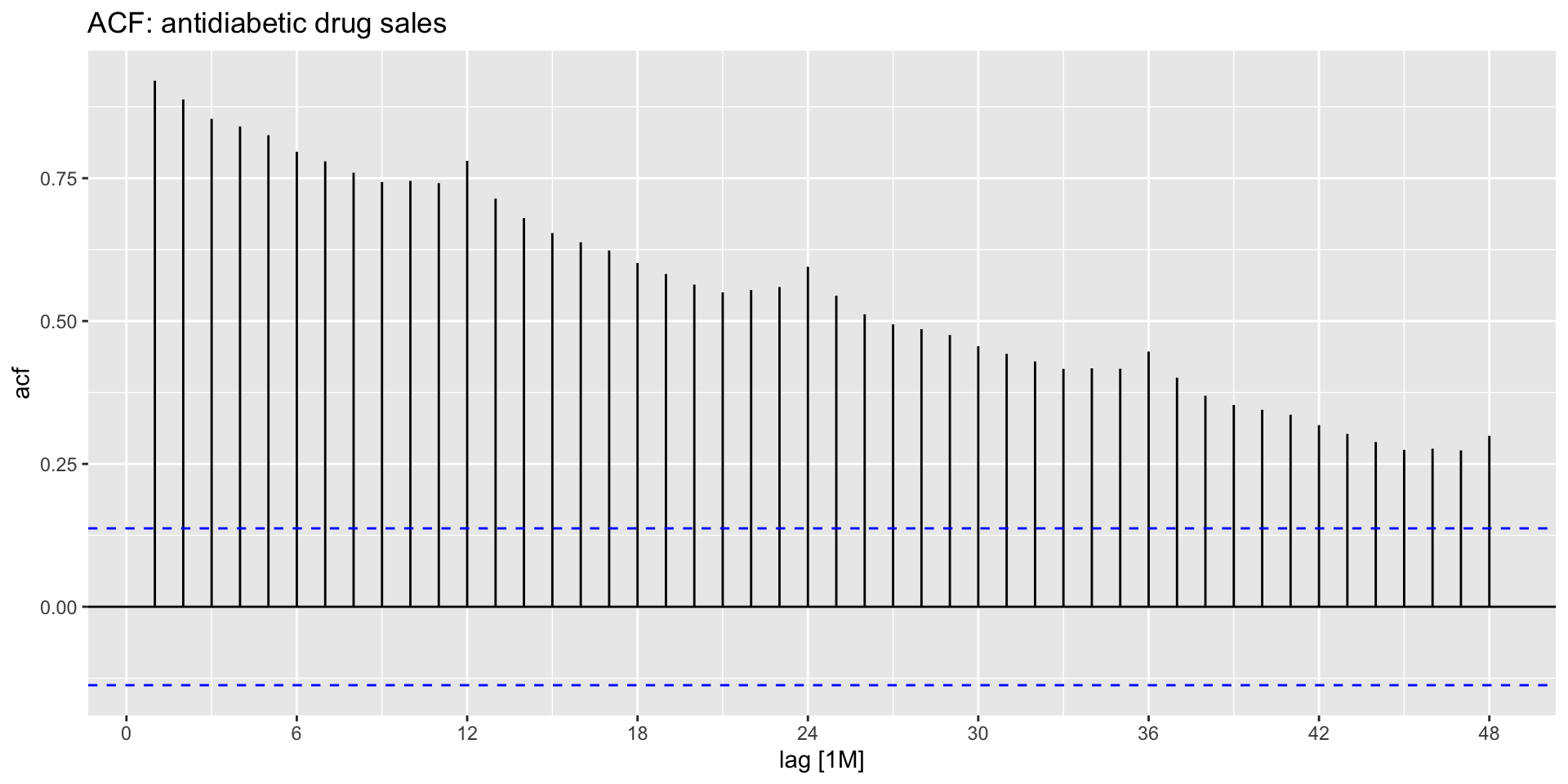
ACF plots in the presence of seasonality

When there is seasonality, \(r_{k}\) tend to be relatively large for the seasonal lags:

White noise

Time series with no or little autocorrelation are called white noise:

y <- tsibble(sample = 1:50, whitenoise = rnorm(50), index = sample)
y |>
  autoplot(whitenoise) +
  labs(title = "White noise")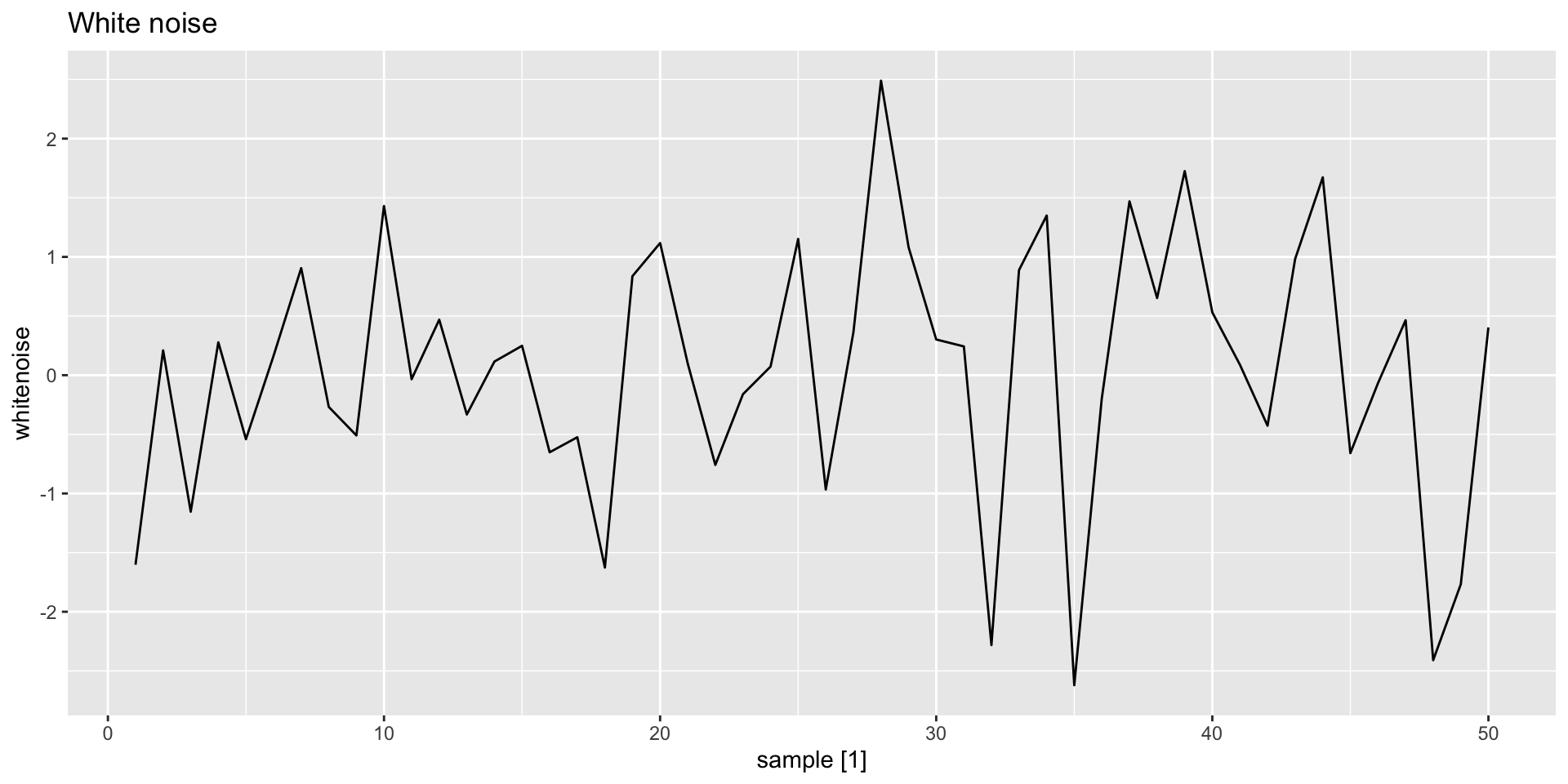

White noise ACF

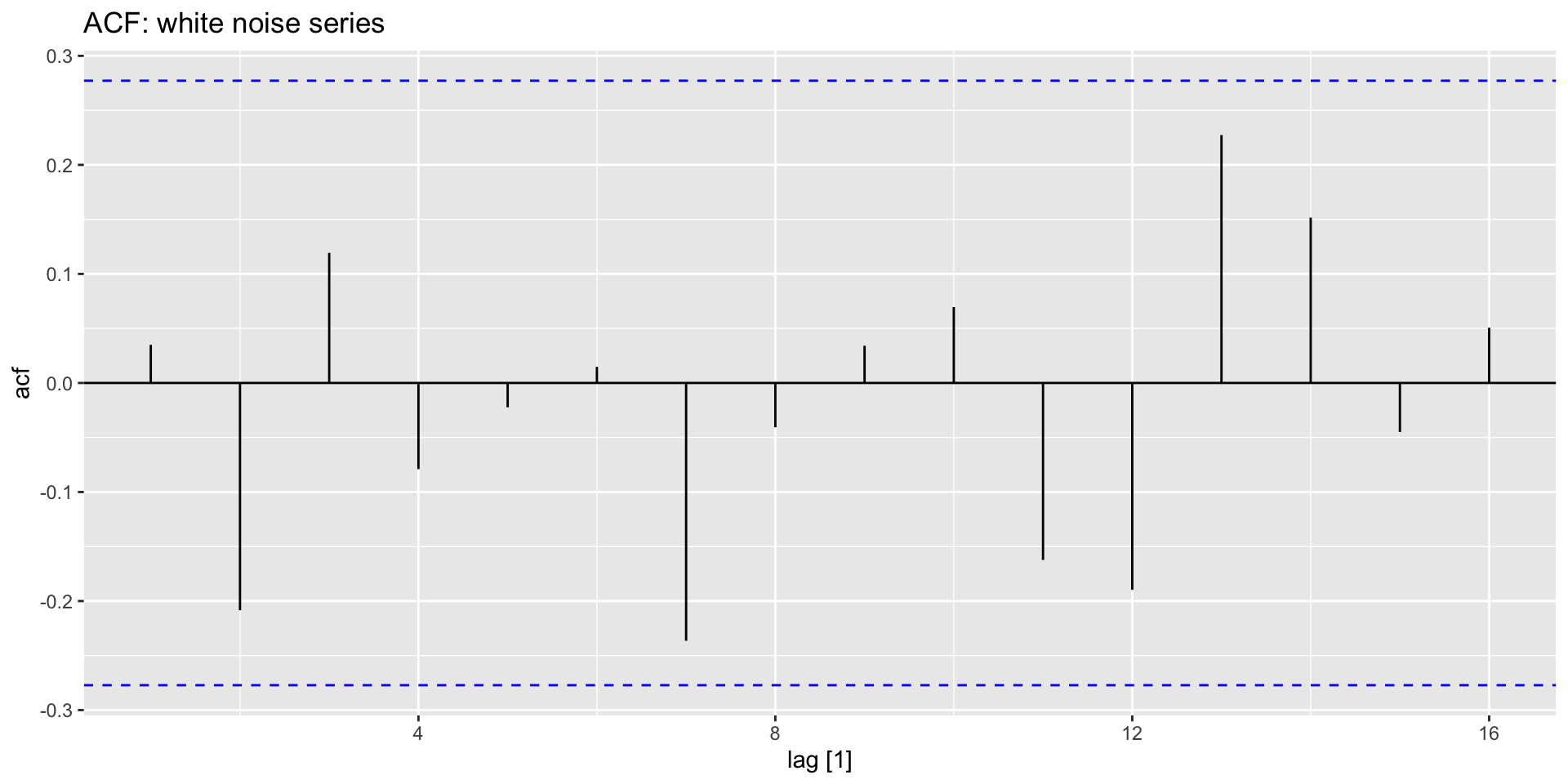
The ACF plot for a white noise series should show \(r_{k}\) of zero on average:

y |>
  ACF(whitenoise) |>
    autoplot() +
    labs(title = "ACF: white noise series")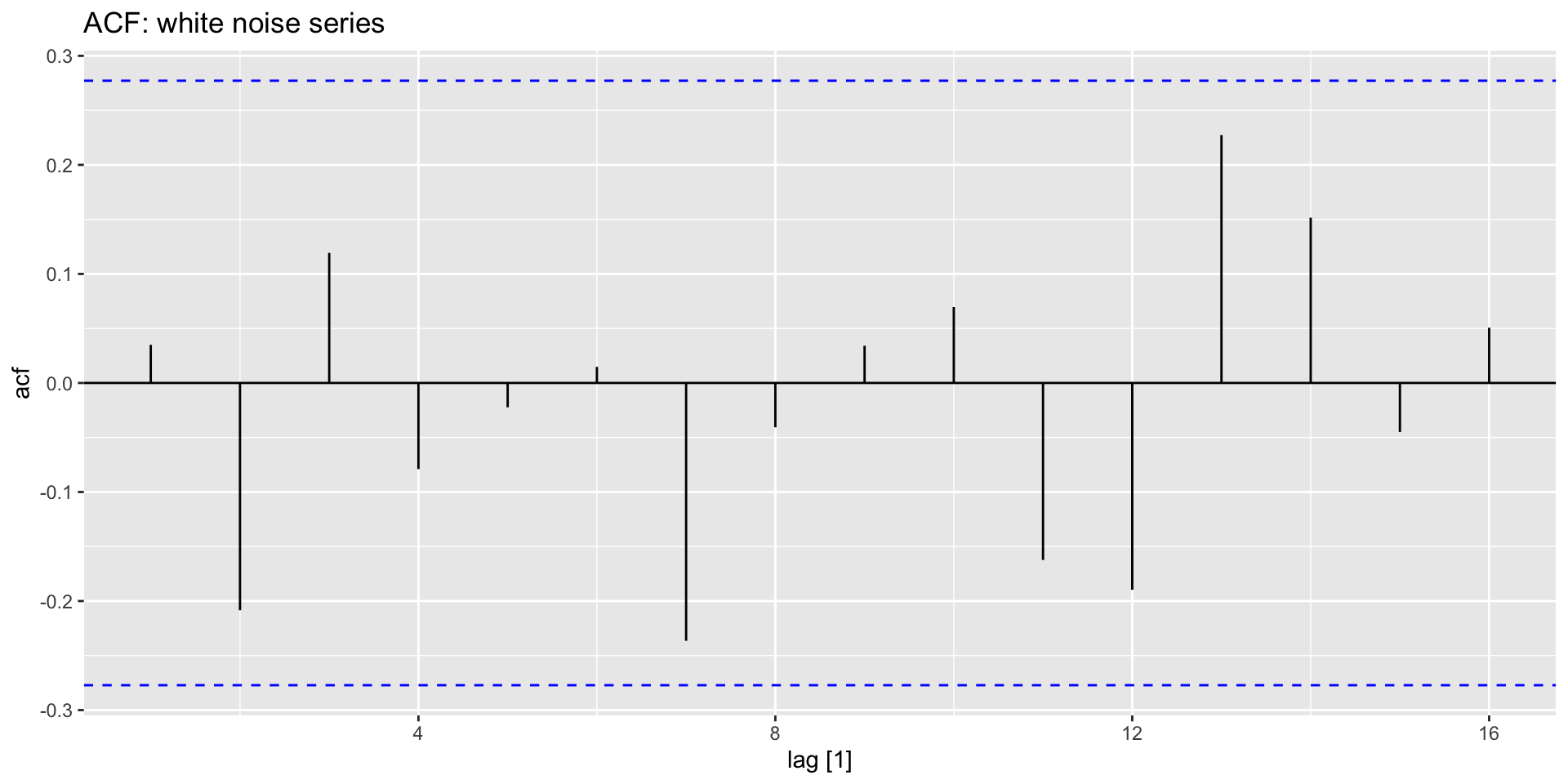

White noise ACF

95% of \(r_{k}\) should lie within \(\pm \frac{1.96}{\sqrt{T}}\).
These bounds are shown in blue below.
Here \(T=50\), so the bounds are at \(\pm \frac{1.96}{\sqrt{50}} = \pm 0.28\). If more then 5% of the “spikes” extend beyond these bounds, it’s not a white noise series.