ARIMA II

BUS 323 Forecasting and Risk Analysis

Moving average models

• Uses past forecast errors:

  \[ y_{t} = c + \epsilon_{t} + \theta_{1} \epsilon_{t-1} + \theta_{2} \epsilon_{t-2} + ... + \theta_{q} \epsilon_{t-q} \]

  • Where \(\epsilon_{t}\) is white noise.
• The above is a MA(q) model.

Moving average models: simulation

• Suppose we have two models:
  • MA(1): \(y_{t} = 20 + \epsilon_{t} + 0.8 \epsilon_{t-1}\).
  • MA(2): \(y_{t} = \epsilon_{t} - \epsilon_{t-1} + 0.8 \epsilon_{t-2}\).
• Generate the MA process for each model based on the following observed values of \(\epsilon_{t}\):

Period	\(\epsilon\)
1	1.712.
2.	-1.514.
3.	0.948.
4.	-1.518.
5.	-0.212.

Moving average models: simulation II

• Suppose we have two models:
  • MA(1): \(y_{t} = 20 + \epsilon_{t} + 0.8 \epsilon_{t-1}\).
  • MA(2): \(y_{t} = \epsilon_{t} - \epsilon_{t-1} + 0.8 \epsilon_{t-2}\).
• Make a 50-observation vector containing white noise. Estimate both of the above MA models.

library(fpp3)
errors <- rnorm(50,0,1)
ma1 <- c(rep(20,length(errors))) + errors + 0.8*difference(errors)
ma2 <- errors - difference(errors) + 0.8*difference(errors,2)

Moving average models: simulation II plot

• Plot the models:

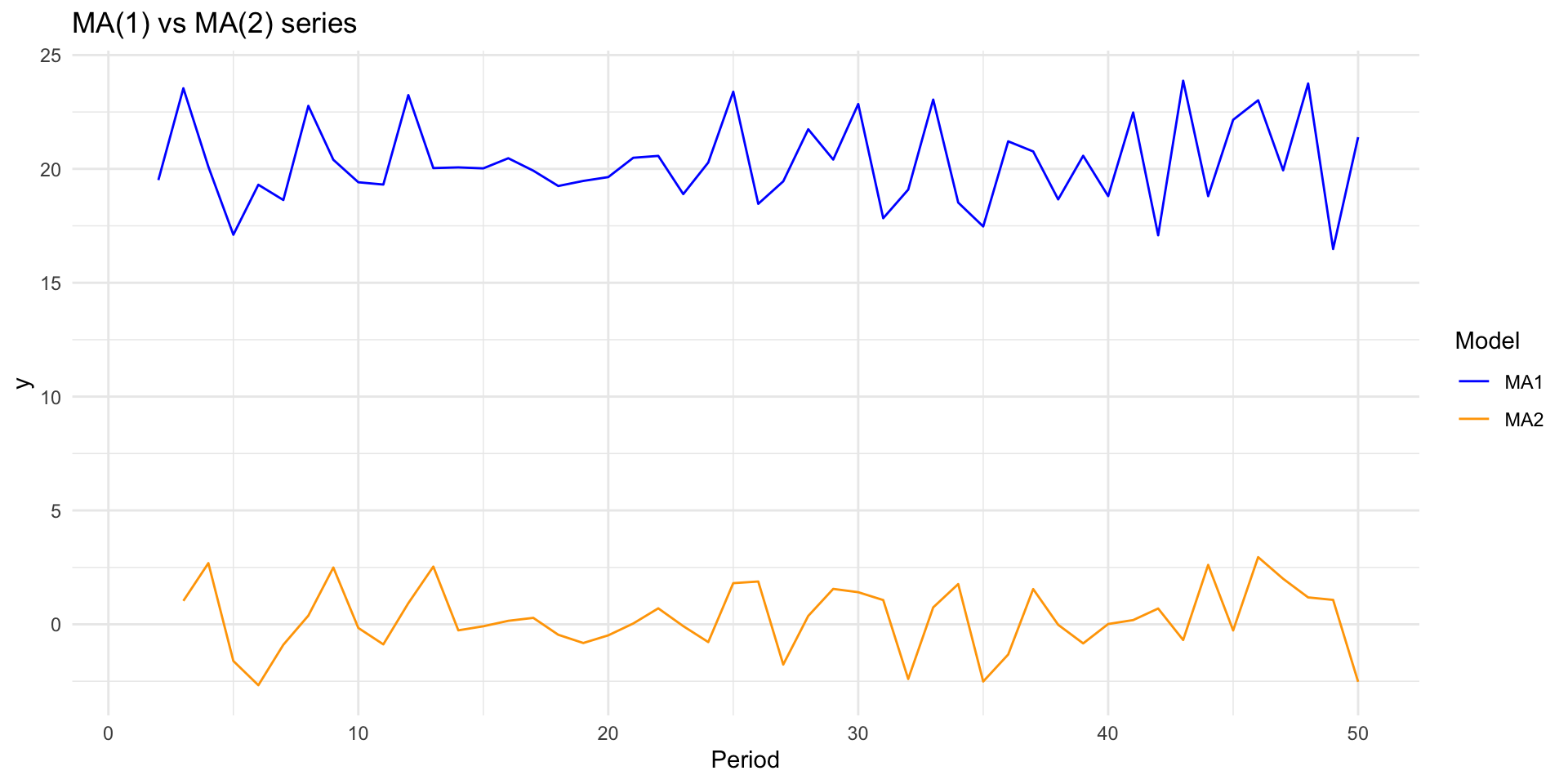
Invertibility

• Any AR(p) model can be expressed as an MA(\(\infty\)) model.
• e.g. for an AR(1):

  \[ \begin{align} y_{t} & = \phi_{1} y_{t-1} + \epsilon_{t} \\ & = \phi_{1}(\phi_{1} y_{t-2} + \epsilon_{t-1}) + \epsilon_{t-1} \\ & = \phi_{1}^{2} y_{t-2} + \phi_{1} \epsilon_{t-1}+ \epsilon_{t} \\ & = \phi_{1}^{2}(\phi_{1} y_{t-3} + \epsilon_{t-2}) + \phi_{1} \epsilon_{t-1} + \epsilon_{t} \\ & = \phi_{1}^{3} y_{t-3} + \phi_{1}^{2} \epsilon_{t-2} + \phi_{1} \epsilon_{t-1} + \epsilon_{t} \\ \textrm{etc.} \end{align} \]

• For \(-1 < \phi_{1} < 1\), \(\phi_{1}^{k}\) decreasing with \(k\).
  • In the limit,

    \[ y_{t} = \epsilon_{t} + \phi_{1} \epsilon_{t-1} + \phi_{1}^{2} \epsilon_{t-2} + \phi_{1}^{3} \epsilon_{t-3} + ... \]

  • An MA(\(\infty\)) process.

ARIMA models

• Combine differencing, autoregression, and moving average models:

  \[ \begin{align} y_{t}' = & c + \phi y_{t-1}' + ... + \phi_{p} y_{t-p}' \\ & + \theta_{1} \epsilon_{t-1} + ... + \theta_{1} \epsilon_{t-q} + \epsilon_{t} \end{align} \]

  • The above is an ARIMA(p,d,q) model

Example: Egyptian exports

• From global_economy:

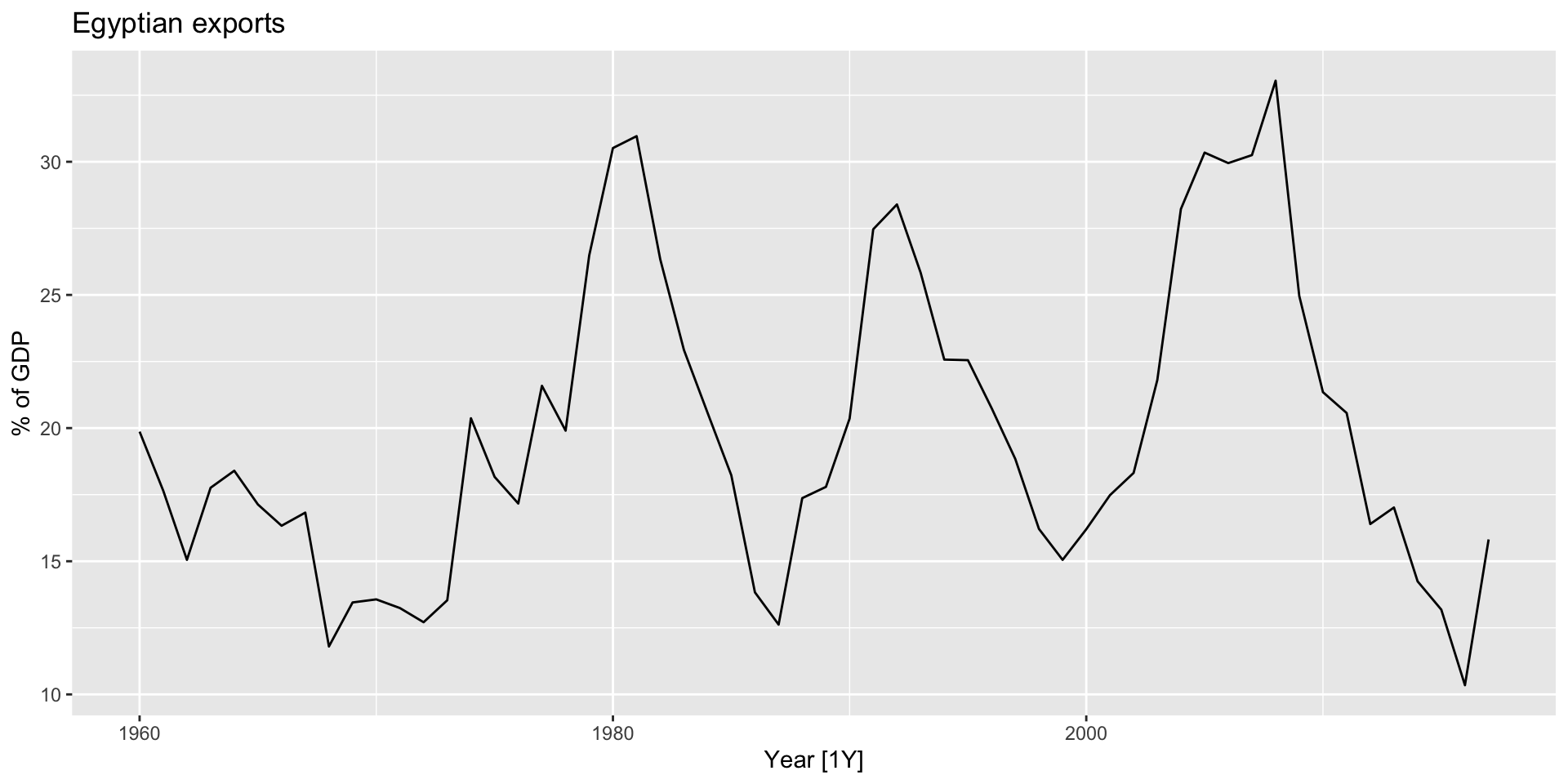
Example: Egyptian exports

• Use ARIMA() to automatically select appropriate values for \(p\), \(d\), and \(q\):

fit <- global_economy |>
  filter(Code == "EGY") |>
  model(ARIMA(Exports))
report(fit)

Series: Exports 
Model: ARIMA(2,0,1) w/ mean 

Coefficients:
         ar1      ar2      ma1  constant
      1.6764  -0.8034  -0.6896    2.5623
s.e.  0.1111   0.0928   0.1492    0.1161

sigma^2 estimated as 8.046:  log likelihood=-141.57
AIC=293.13   AICc=294.29   BIC=303.43

Example: Egyptian exports

• Forecast 10 years into the future:

fit |> forecast(h=10) |>
  autoplot(global_economy) +
  labs(y = "% of GDP", title = "Egyptian exports")

Example: Egyptian exports

• Forecast 10 years into the future:

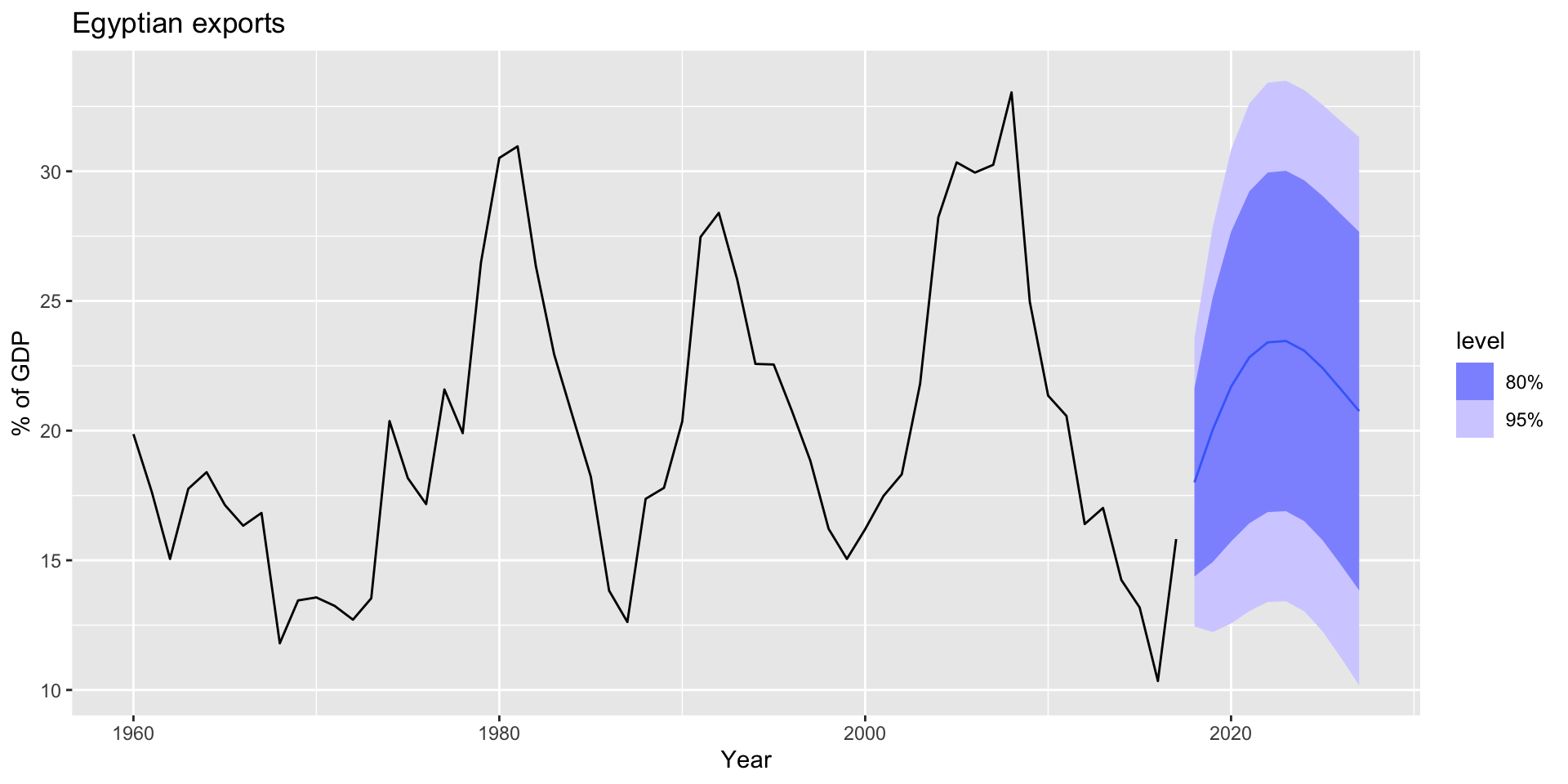
Notable parameter values

• If \(c=0\) and \(d=0\), forecasts \(\rightarrow\) 0.
• If \(c=0\) and \(d=1\), forecasts \(\rightarrow\) non-zero constant.
• If \(c=0\) and \(d=2\), forecasts \(\rightarrow\) straight line.
• If \(c \neq 0\) and \(d=0\), forecasts \(\rightarrow \bar{y}\).
• If \(c \neq 0\) and \(d=1\), forecasts \(\rightarrow\) straight line.
• If \(c \neq 0\) and \(d=2\), forecasts \(\rightarrow\) quadratic trend (this is bad)
• To obtain cyclic forecasts, \(p \geq 2\).