Exponential smoothing

BUS 323 Forecasting and Risk Analysis

Simple exponential smoothing

Naive method:

\[ \widehat{y}_{T+h|T} = y_{T} \]
- All weight given to observation \(T\)
Mean method:

\[ \widehat{y}_{T+h|T} = \frac{\sum_{t=1}^{T}y_{t}}{T} \]
- All observations equally weighted

Simple exponential smoothing

We might want something in between.
- More weight to recent observations
- Less weight to those in the distant past
Simple exponential smoothing

\[ \widehat{y}_{T+1|T} = \alpha y_{T} + \alpha(1-\alpha) y_{T-1} + \alpha(1-\alpha)^{2} y_{T-2} + ... \]
- \(0 \leq \alpha \leq 1\): smoothing parameter

Optimization

Need to estimate \(\alpha\) and \(l_{0}\).
As with regression, seek to minimize SSE (sum of squared errors):

\[ SSE = \sum_{t=1}^{T} (y_{t} - \widehat{y}_{t|t-1})^{2} = \sum_{t=1}^{t} e_{t}^{2} \]
No OLS SSE-minimizing formulae here

Example: Algerian exports

Simple exponential smoothing works best with data with no trend or seasonality.

library(fpp3)
algeria_economy <- global_economy |>
  filter(Country == "Algeria")
algeria_economy |>
  autoplot(Exports) +
  labs(y = "% of GDP", title = "Exports: Algeria")

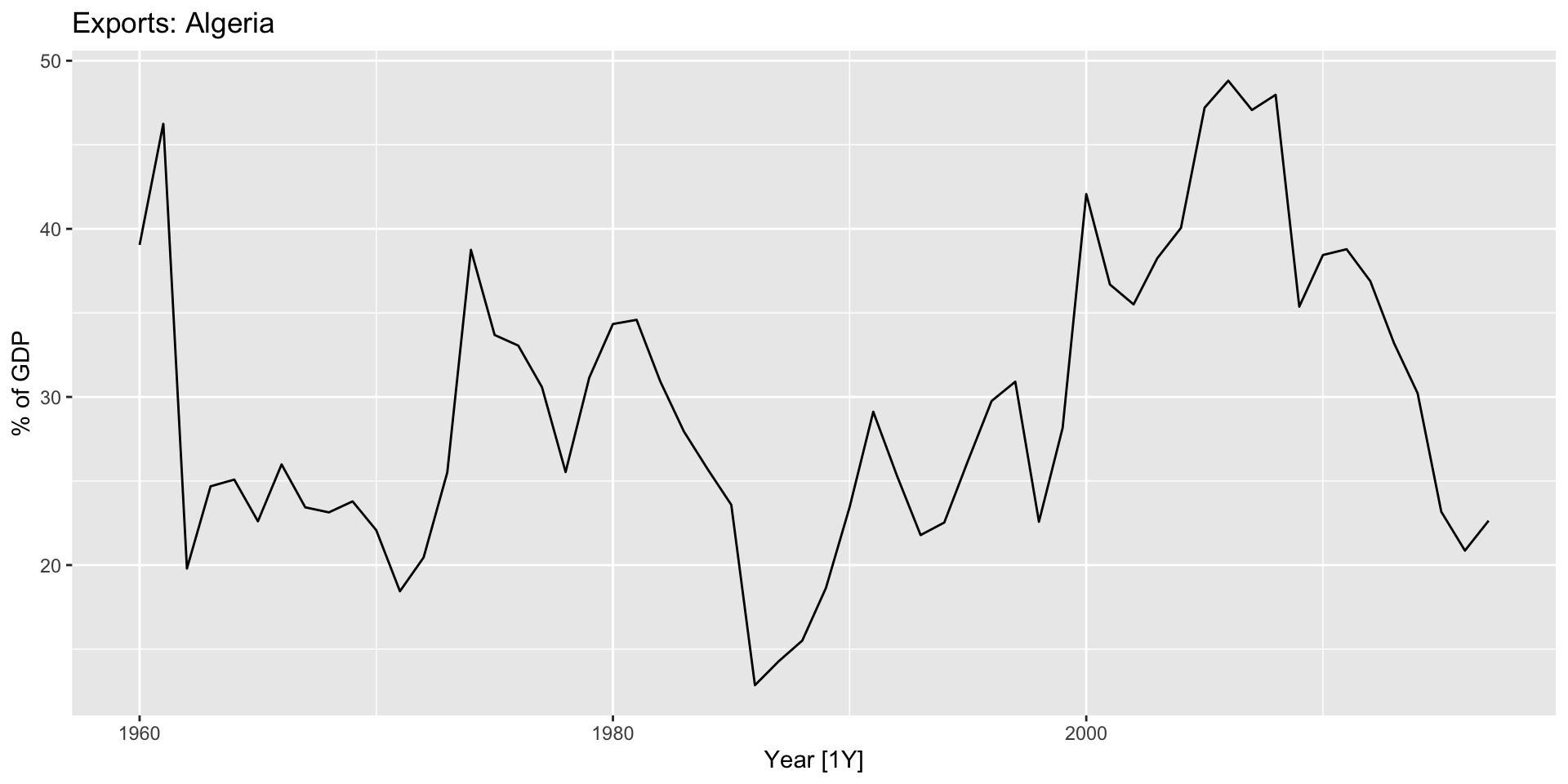
Example: Algerian exports

To estimate an exponential smoothing model, use the ETS() option in model():

fit <- algeria_economy |>
  model(ets_model = ETS(Exports ~ error("A") + trend("N") + season("N")))
# extract parameters
fit$ets_model[[1]]$fit$par

# A tibble: 2 × 2
  term  estimate
  <chr>    <dbl>
1 alpha    0.840
2 l       39.5

Example: Algerian exports

Produce a 5-step forecast:

fc <- fit |>
  forecast(h = 5)

Example: Algerian exports

Plot forecast + historical data:

fc |>
  autoplot(algeria_economy) +
  geom_line(aes(y = .fitted), col="#D55E00",
            data = augment(fit)) +
  labs(y="% of GDP", title="Exports: Algeria") +
  guides(colour = "none")

Example: Algerian exports

Plot forecast + historical data:

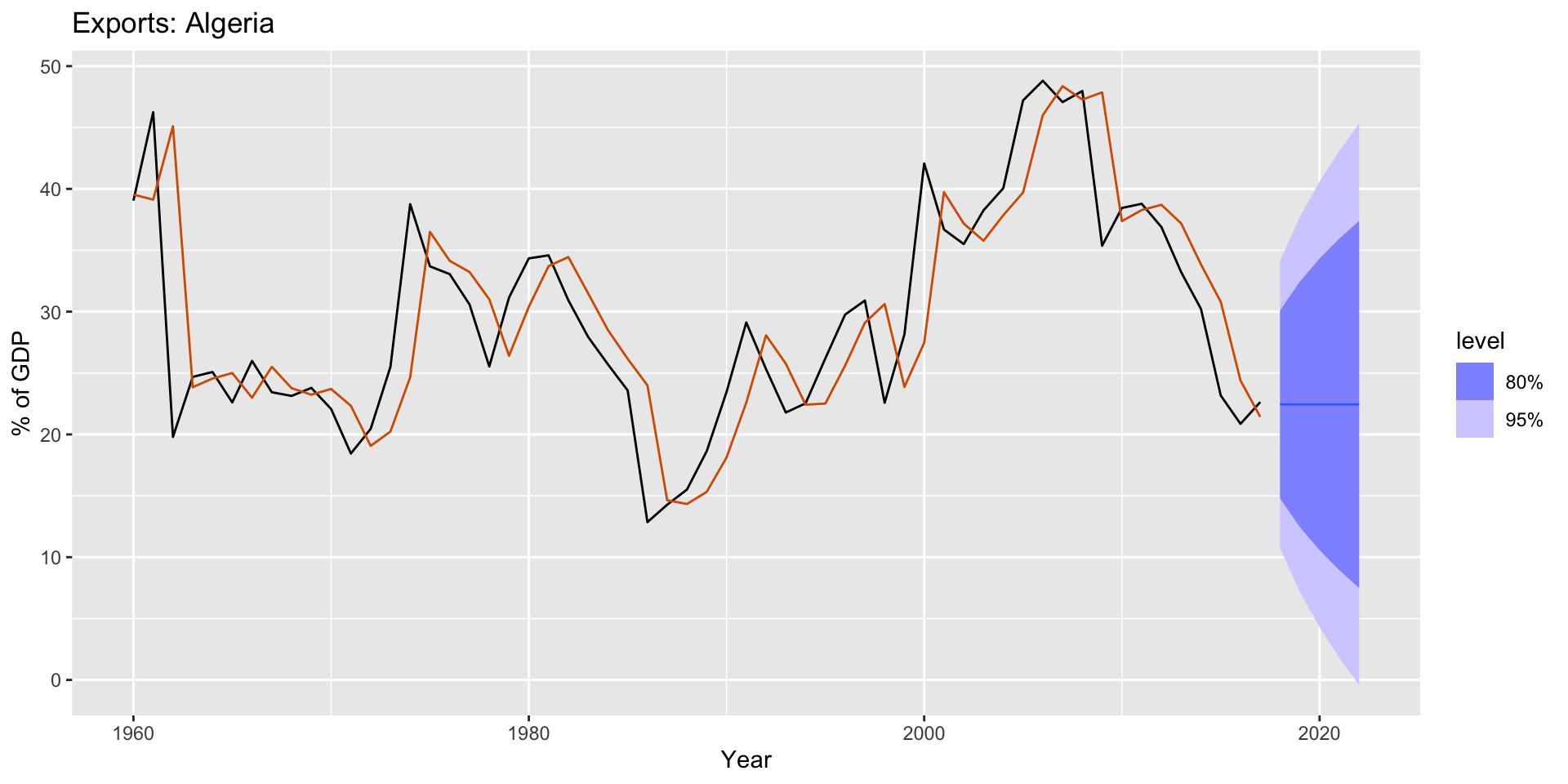
Exponential smoothing with trend

Holt’s linear trend method:

\[ \begin{align} \textrm{Forecast equation. } & \widehat{y}_{t+h|t} = l_{t} + hb_{t} \end{align} \]

\[ \begin{align} \textrm{Level equation. } & l_{t} = \alpha y_{t} + (1-\alpha)(l_{t-1} + b_{t-1}) \end{align} \]

\[ \begin{align} \textrm{Trend equation. } & b_{t} = \beta^{*} (l_{t} - l_{t-1}) + (1-\beta^{*})b_{t-1} \end{align} \]
- \(l_{t}\): level of \(y\) at \(t\)
- \(b_{t}\): trend of \(y\) at \(t\)
- \(\alpha\): smoothing parameter for level
- \(\beta^{*}\): smoothing parameter for trend

Example: Australian population

Use a series with a trend:

aus_economy <- global_economy |>
  filter(Code == "AUS") |>
  mutate(Pop = Population / 1e6)
autoplot(aus_economy, Pop) +
  labs(y = "Millions", title = "Australian population")

Example: Australian population

Use a series with a trend:

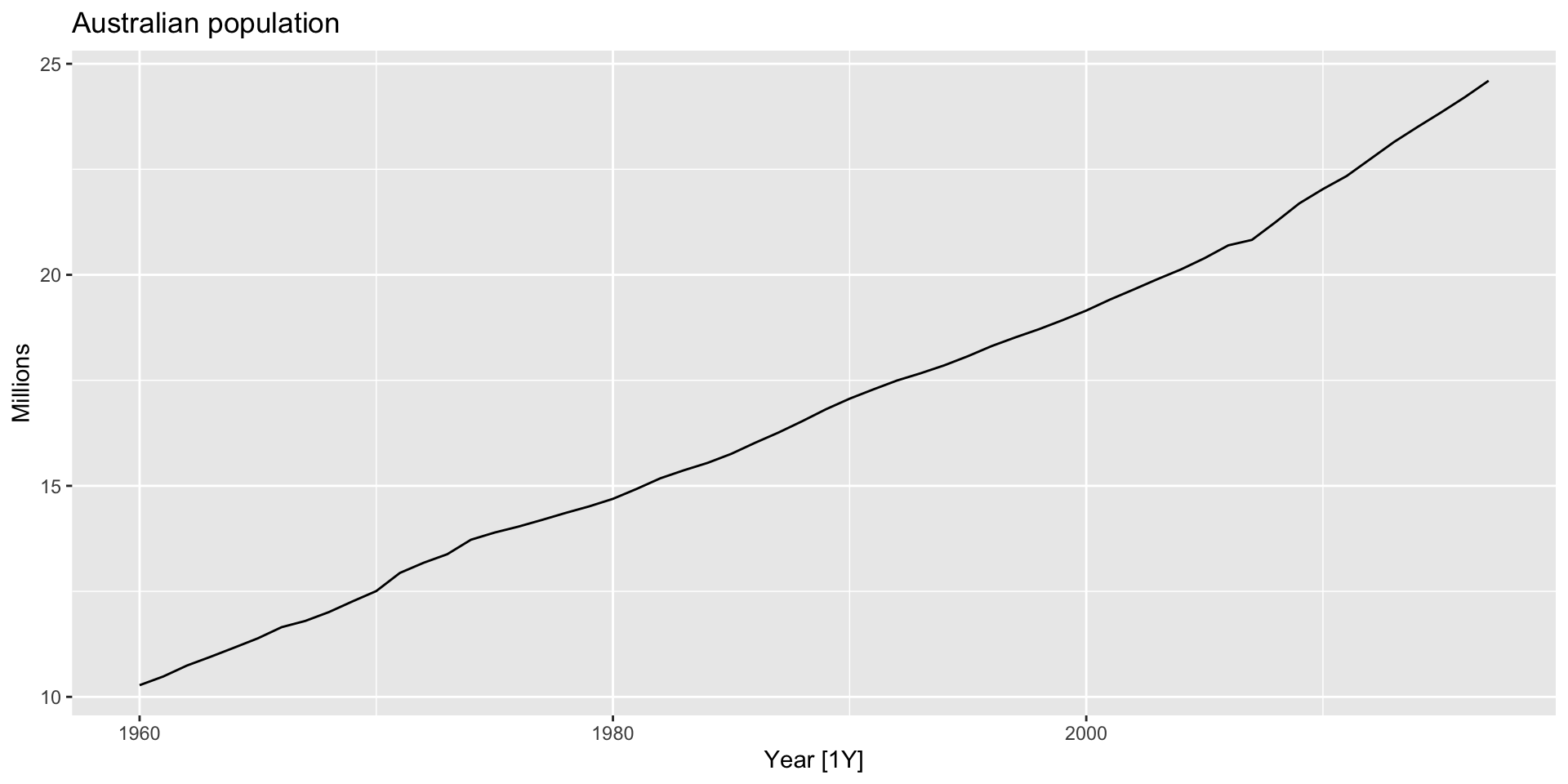
Example: Australian population

Apply Holt’s method by using the trend("A") option within model(ETS()).
- \(\alpha\), \(\beta^{*}\), \(l_{0}\), \(b_{0}\) estimated by minimizing SSE for one-step training errors.

fit <- aus_economy |>
  model(
    AAN = ETS(Pop ~ error("A") + trend("A") + season("N"))
  )
fit$AAN[[1]]$fit$par

# A tibble: 4 × 2
  term  estimate
  <chr>    <dbl>
1 alpha    1.000
2 beta     0.327
3 l       10.1  
4 b        0.222

Damped trend methods

Gardner-McKenzie method:

\[ \widehat{y}_{t+h|t} = l_{t} + (\phi + \phi^{2} + ... + \phi^{h})b_{t} \]
- \(0 < \phi < 1\): damping parameter
  
  \[ l_{t} = \alpha y_{t} + (1-\alpha)(l_{t-1} + \phi b_{t-1}) \]
  
  \[ b_{t} = \beta^{*}(l_{t}-l_{t-1}) + (1-\beta^{*}) \phi b_{t-1} \]
- Forecasts converge to \(l_{T} + \frac{\phi b_{T}}{1-\phi}\) in the limit of \(h\)
- Long-run forecasts: constant
- Short-run forecasts: trended
Usually \(0.8 \leq \phi \leq 0.98\).

Example: Australian population

Compare a trended model to a damped trended model (use \(\phi=0.9\)). Estimate 15-step forecasts:

aus_economy |>
  model(
    `Holt's method` = ETS(Pop ~ error("A") +
                       trend("A") + season("N")),
    `Damped Holt's method` = ETS(Pop ~ error("A") +
                       trend("Ad", phi = 0.9) + season("N"))
  ) |>
  forecast(h=15)

# A fable: 30 x 5 [1Y]
# Key:     Country, .model [2]
   Country   .model         Year
   <fct>     <chr>         <dbl>
 1 Australia Holt's method  2018
 2 Australia Holt's method  2019
 3 Australia Holt's method  2020
 4 Australia Holt's method  2021
 5 Australia Holt's method  2022
 6 Australia Holt's method  2023
 7 Australia Holt's method  2024
 8 Australia Holt's method  2025
 9 Australia Holt's method  2026
10 Australia Holt's method  2027
# ℹ 20 more rows
# ℹ 2 more variables: Pop <dist>, .mean <dbl>

Example: Australian population

And plot:

aus_economy |>
  model(
    `Holt's method` = ETS(Pop ~ error("A") +
                       trend("A") + season("N")),
    `Damped Holt's method` = ETS(Pop ~ error("A") +
                       trend("Ad", phi = 0.9) + season("N"))
  ) |>
  forecast(h = 15) |>
  autoplot(aus_economy, level = NULL) +
  labs(title = "Australian population",
       y = "Millions") +
  guides(colour = guide_legend(title = "Forecast"))

Example: Australian population

And plot:

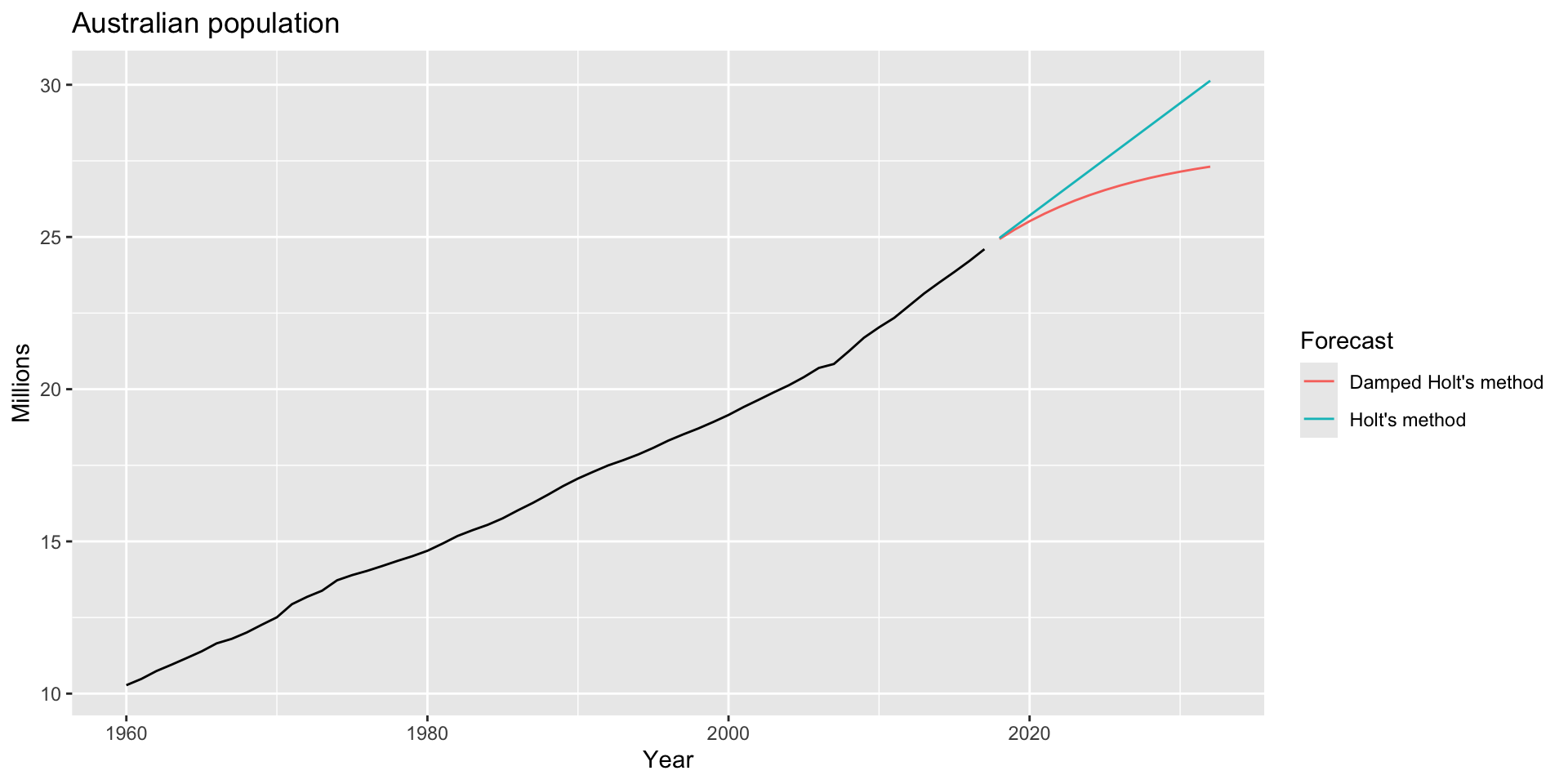
Example: internet usage

Which method works best for these data?

www_usage <- as_tsibble(WWWusage)
www_usage |> autoplot(value) +
  labs(x="Minute", y="Number of users",
       title = "Internet usage per minute")

Example: internet usage

Which method works best for these data?

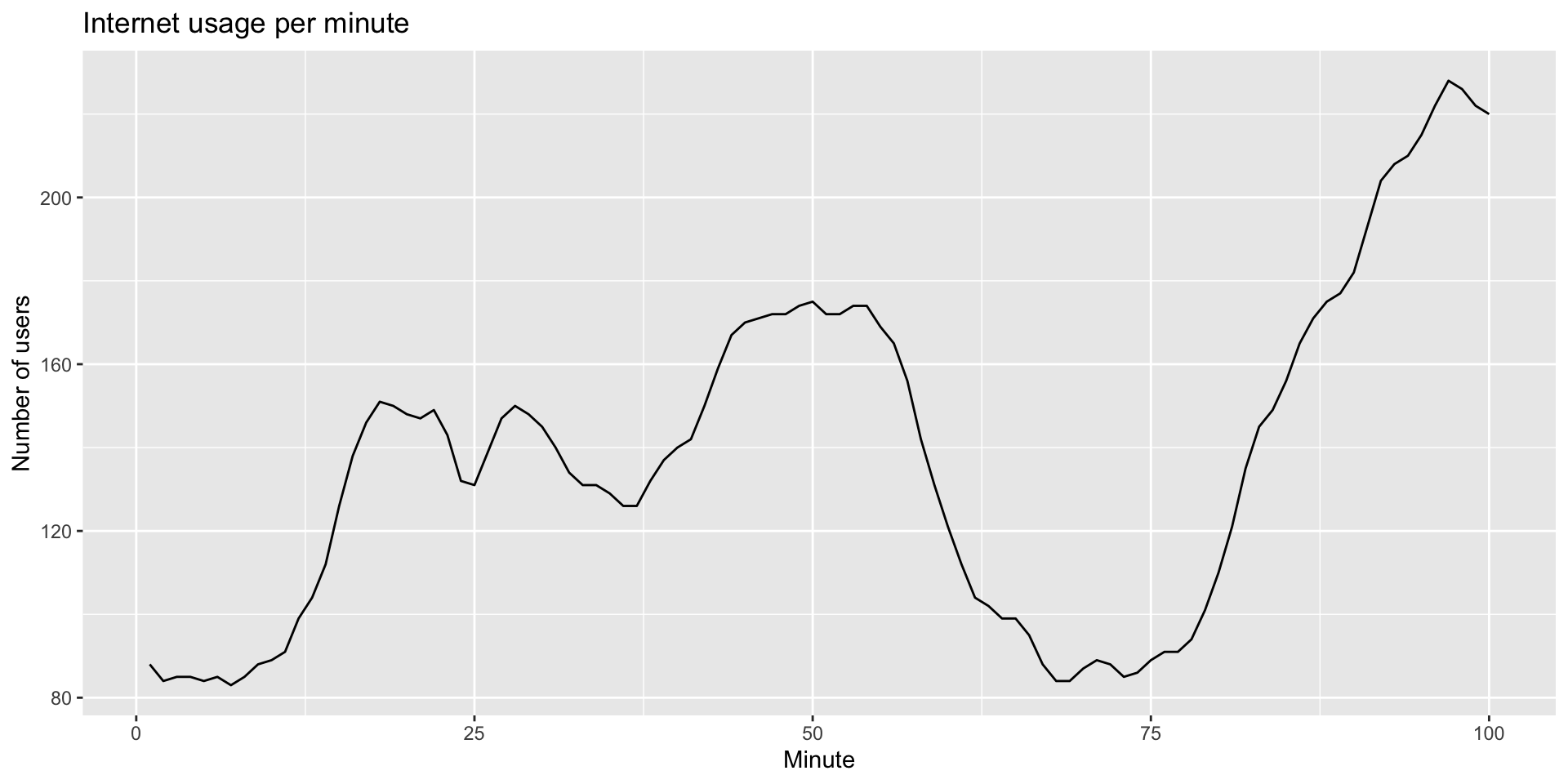
Example: internet usage

Estimate a 1-step forecast for all three smoothing methods.
Use cross-validation (use an initial sample of size 10) to evaluate accuracy.

www_usage |>
  stretch_tsibble(.init = 10) |>
  model(
    SES = ETS(value ~ error("A") + trend("N") + season("N")),
    Holt = ETS(value ~ error("A") + trend("A") + season("N")),
    Damped = ETS(value ~ error("A") + trend("Ad") +
                   season("N"))
  ) |>
  forecast(h = 1) |>
  accuracy(www_usage)

# A tibble: 3 × 10
  .model .type     ME  RMSE   MAE   MPE  MAPE  MASE RMSSE  ACF1
  <chr>  <chr>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Damped Test  0.288   3.69  3.00 0.347  2.26 0.663 0.636 0.336
2 Holt   Test  0.0610  3.87  3.17 0.244  2.38 0.701 0.668 0.296
3 SES    Test  1.46    6.05  4.81 0.904  3.55 1.06  1.04  0.803

Example: internet usage

Use the best-performing method to forecast 10 steps into the future. Estimate:

fit <- www_usage |>
  model(
    Damped = ETS(value ~ error("A") + trend("Ad") +
                   season("N"))
  )
tidy(fit)

# A tibble: 5 × 3
  .model term  estimate
  <chr>  <chr>    <dbl>
1 Damped alpha   1.000 
2 Damped beta    0.997 
3 Damped phi     0.815 
4 Damped l[0]   90.4   
5 Damped b[0]   -0.0173

Example: internet usage

Forecast:

fit |>
  forecast(h = 10) |>
  autoplot(www_usage) +
  labs(x="Minute", y="Number of users",
       title = "Internet usage per minute")